1.12:
Dimensionsanalyse
1.12:
Dimensionsanalyse
Dimensional analysis, also known as the factor label method, is a versatile approach for mathematical operations. The main principle behind this approach is: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method can be applied to computations ranging from simple unit conversions to more complex and multi-step calculations involving several different quantities and their units.
Conversion Factors and Dimensional Analysis
The unit conversion factor is a ratio of two equivalent quantities expressed with different measurement units. For example, 1.0936 yards and 1 meter measure the same length (by definition, 1.0936 yd = 1 m). Thus, to convert between these two equivalent units, a unit conversion factor is derived from the ratio
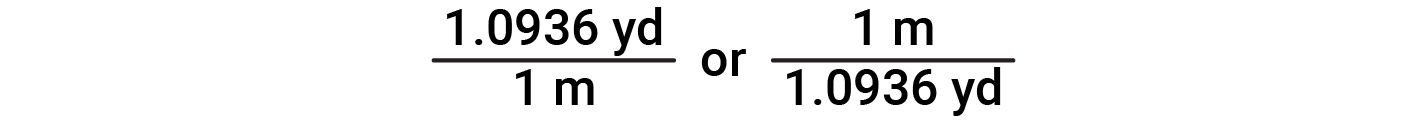
When a quantity (such as distance in yards) is multiplied or divided by an appropriate unit conversion factor, the quantity is converted to an equivalent value with different units (such as distance in meters). For example, a 25.0 m long lawn can be converted to yards by multiplying it with the appropriate conversion factor

Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. As the numbers of these two quantities are multiplied to yield the number of the product quantity, 27.3, similarly, the units are multiplied. Just as for numbers, a ratio of identical units is also numerically equal to one, and the unit product thus simplifies to yd. When identical units divide to yield a factor of 1, they are said to “cancel.”
Dimensional analysis may be used to confirm the proper application of unit conversion factors. Consider a 500 cm tall giraffe. To calculate the height in meters, the correct conversion factor must be used, which should cancel all other units except meters. The unit conversion factor for lengths in terms of meters and centimeters may be represented as

The correct unit conversion factor is the ratio that cancels the units of centimeters and provides an answer in meters.

Unit Conversion With Units Raised to a Power
While applying conversion factors for units raised to a power, both the number and the unit are raised to the same power. For example, to convert from yd2 to m2, the relationship between yd and m is used.
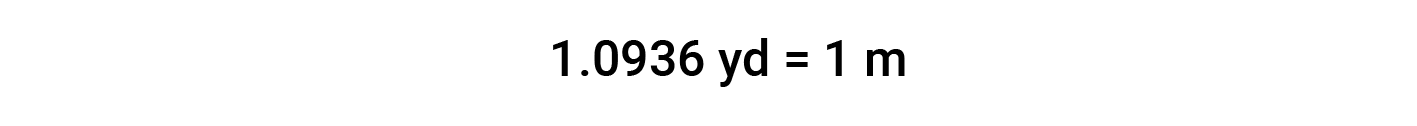
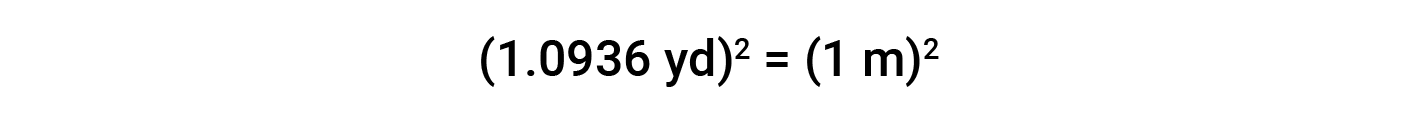
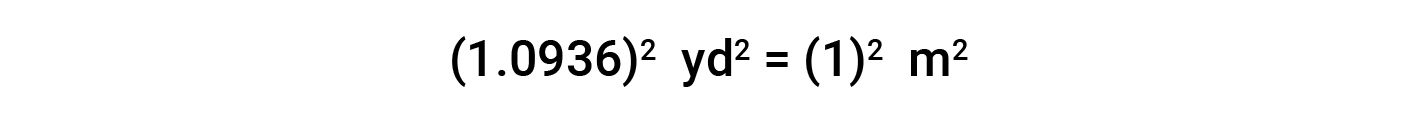
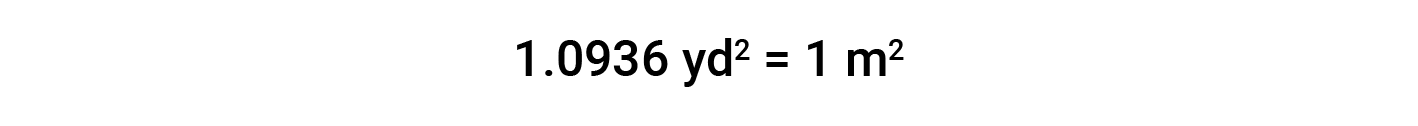
Beyond simple unit conversions, the factor-label method can be used to solve more complex problems involving computations. The basic approach is the same—all the factors involved in the calculation must be appropriately oriented to ensure that their units will appropriately cancel and/or combine to yield the desired unit in the result.
This text has been adapted from Openstax, Chemistry 2e, Section 1.6: Mathematical Treatment of Measurement Results.
