11.9:
克劳修斯-克拉伯龙方程(Clausius-Clapeyron Equation)
A subscription to JoVE is required to view this content. Sign in or start your free trial.
JoVE Core
Chemistry
Clausius-Clapeyron Equation
记得液体的蒸气压 会随着温度的升高而增加。但是,这种依赖性不是线性的。举例来说,水在 50 摄氏度时的蒸气压是 0.122 atm,而在 100 摄氏度时 为 1 atm。蒸气压曲线随着温度的升高 而急剧向上弯曲,从而形成指数曲线。相比之下,当将蒸气压的自然对数 相对于温度倒数作图时,可获得一条直线,其方程式称为 克劳修斯—克拉珀龙方程。此处的 R 为理想气体常数。c,液体的恒定特性,是 y 轴截距;直线的斜率等于摩尔蒸发热 与气体常数 的负比值。根据平衡蒸气压和温度的实验测量值,利用该方程式 可计算出 摩尔蒸发热。例如,假设乙醇蒸气压的自然对数 相对于温度倒数作图,得出直线,斜率为负 4638 开尔文。结合方程式、直线斜率 和 R 值可得出 乙醇的摩尔蒸发热为 38560 焦耳每摩尔。如果已知任何一种液体的 摩尔蒸发热及其在一个温度下的蒸气压,则可用该方程的两点形式 来计算该液体 在不同温度下的蒸气压。以水为例,水的蒸发焓为 每摩尔 40.7 千焦耳。如果水在 373 开尔文的蒸汽压是 1 atm,那么在 383 开尔文时水的蒸汽压是多少?为了解决该问题,使用方程的两点形式,替换给定的 蒸气压、蒸发焓、两个温度和气体常数值,得到 383 开尔文时的 水蒸气压为 1.409 atm。温度从 373 开尔文上升到 383 开尔文,蒸气压上升 0.409 atm,这清楚地表明 蒸气压随温度的增加变化是 一个非线性过程。
11.9:
克劳修斯-克拉伯龙方程(Clausius-Clapeyron Equation)
液体及其蒸汽之间的平衡取决于系统的温度;温度升高会导致其液体的蒸汽压相应升高。 克劳修斯-克拉伯龙方程(Clausius-Clapeyron Equation) 给出了一种物质的蒸汽压 (P) 与其温度 (T) 之间的定量的关系;它预测了每单位温度升高时蒸汽压的升高速度。
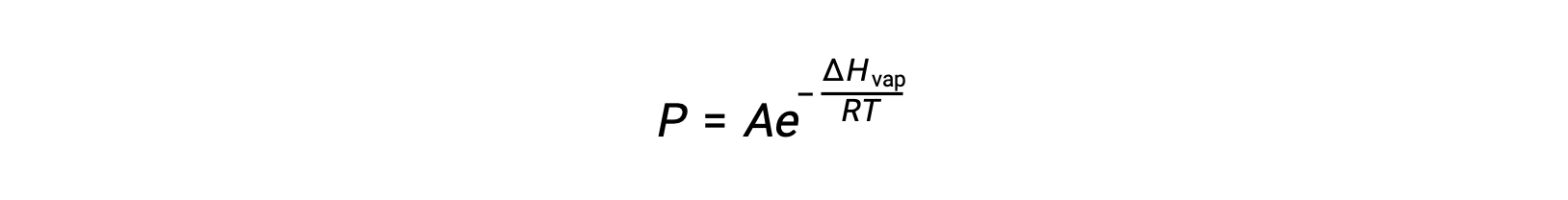
其中, ΔHvap 是液体汽化的焓, R 是气体常数, A 是一个常数,其值取决于物质的化学特性。 温度 (T) 必须在此方程式中以开氏为单位。 但是,由于蒸汽压和温度之间的关系不是线性的,因此公式通常重新排列为对数形式,以产率线性公式:
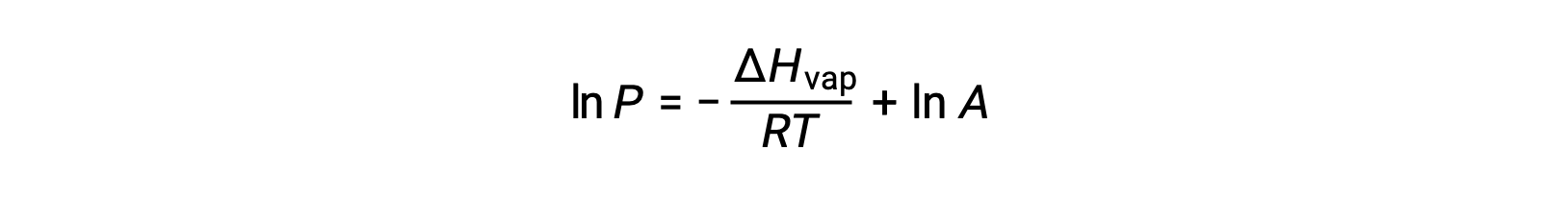
对于任何液体,如果已知特定温度下汽化和蒸汽压的焓, 克劳修斯-克拉伯龙方程(Clausius-Clapeyron Equation) 允许在不同温度下确定液体的蒸汽压。 为此,线性方程式可以两点格式表示。 如果在温度 T1 时蒸汽压为 P1 ,而在温度 T2 时蒸汽压为 P2 ,则相应的线性方程式为:
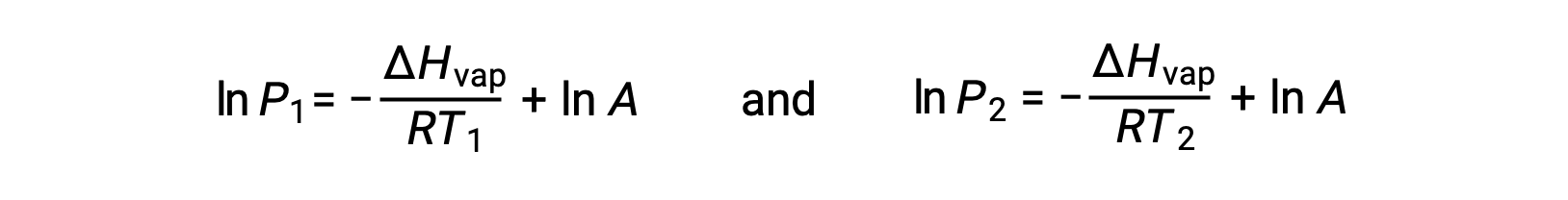
由于常量 A 相同,可以重新排列这两个方程式以隔离 ln a ,然后将它们设置为彼此相等:
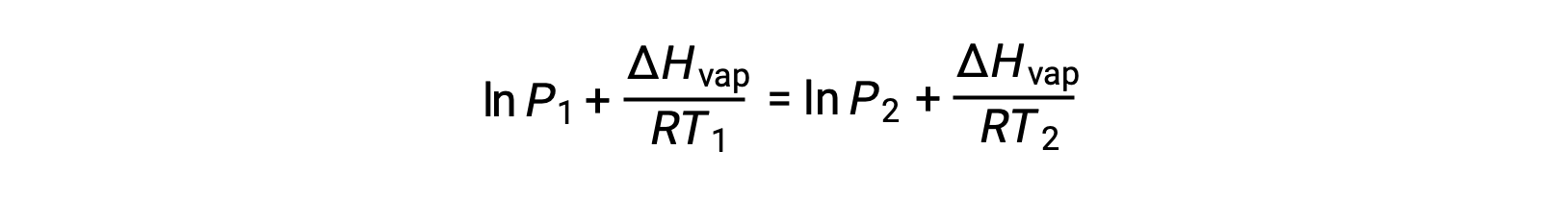
可组合到:
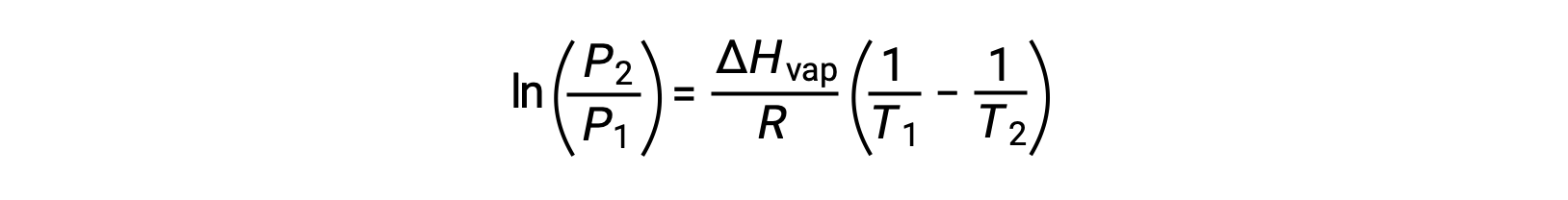
本文改编自 Openstax, 化学 2e, 第10.3节:相变。
