11.9: Equação de Clausius-Clapeyron
O equilíbrio entre um líquido e o seu vapor depende da temperatura do sistema; um aumento da temperatura provoca um aumento correspondente da pressão de vapor do seu líquido. A equação de Clausius-Clapeyron fornece a relação quantitativa entre a pressão de vapor de uma substância (P) e a sua temperatura (T); ela prevê a taxa à qual a pressão de vapor aumenta por unidade de aumento da temperatura.
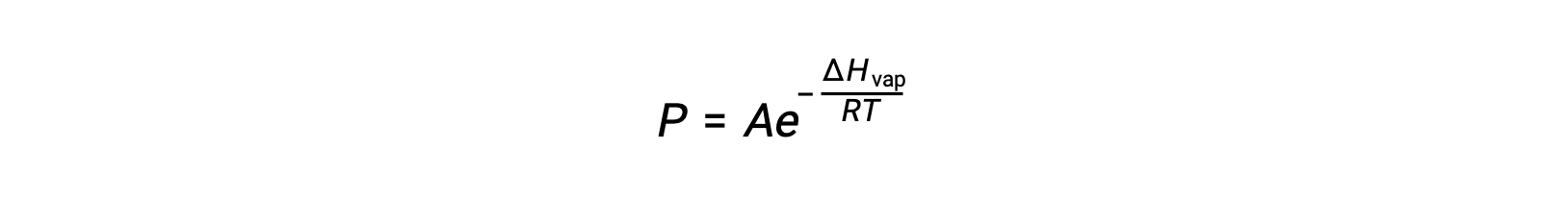
onde ΔHvap é a entalpia de vaporização para o líquido, R é a constante de gás, e A é uma constante cujo valor depende da identidade química da substância. A temperatura (T) deve estar em kelvin nesta equação. No entanto, como a relação entre pressão de vapor e temperatura não é linear, a equação é frequentemente rearranjada em forma logarítmica para produzir a equação linear:
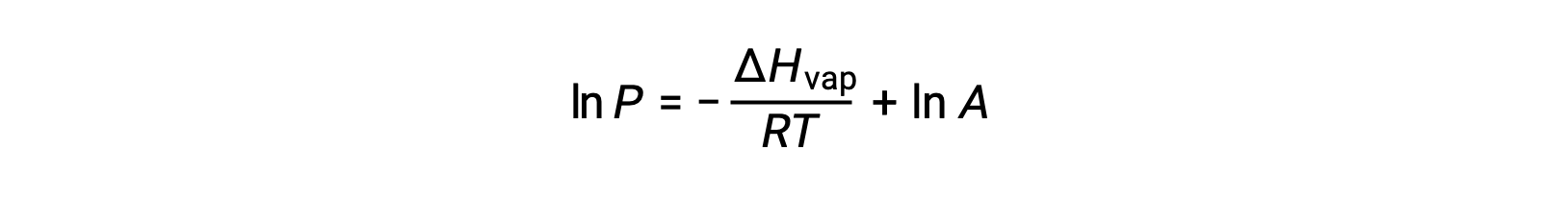
Para qualquer líquido, se for conhecida a entalpia da vaporização e a pressão de vapor a uma determinada temperatura, a equação de Clausius-Clapeyron permite determinar a pressão de vapor do líquido a uma temperatura diferente. Para isso, a equação linear pode ser expressa em formato de dois pontos. Se, à temperatura T1, a pressão de vapor for P1, e à temperatura T2, a pressão de vapor for P2, as equações lineares correspondentes são:
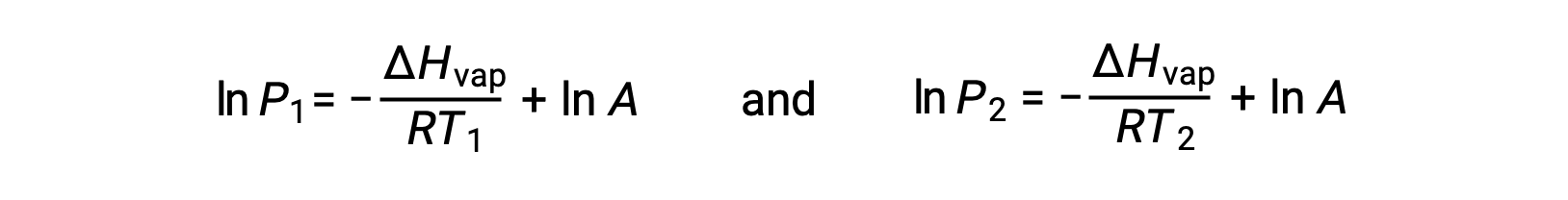
Como a constante, A, é a mesma, essas duas equações podem ser rearranjadas para isolar ln A e defini-las então iguais uma à outra:
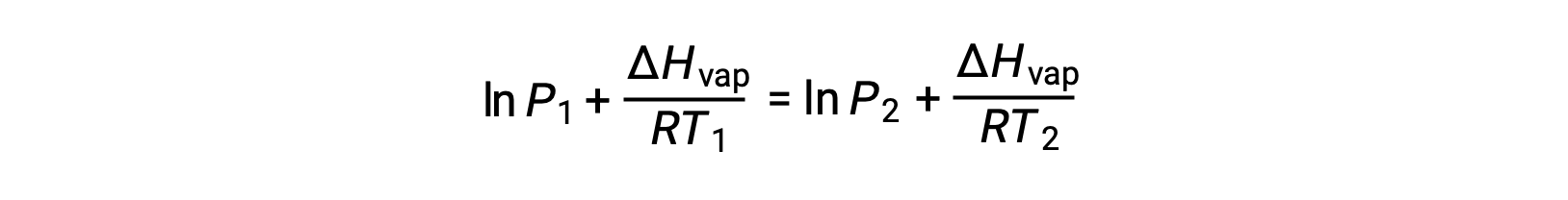
o que pode ser combinado em:
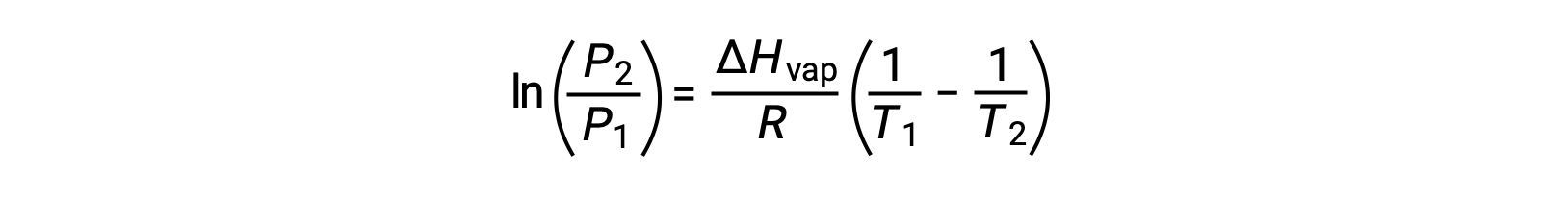
Este texto é adaptado de Openstax, Chemistry 2e, Section 10.3: Phase Transitions.


