11.9:
Clausius-Clapeyron Denklemi
11.9:
Clausius-Clapeyron Denklemi
Bir sıvı ile buharı arasındaki denge, sistemin sıcaklığına bağlıdır; sıcaklıktaki bir artış, sıvısının buhar basıncında buna karşılık gelen bir artışa neden olur. Clausius-Clapeyron denklemi, bir maddenin buhar basıncı (P) ile sıcaklığı (T) arasındaki nicel ilişkiyi verir; Sıcaklıkta birim artış başına buhar basıncının artma oranını tahmin eder.
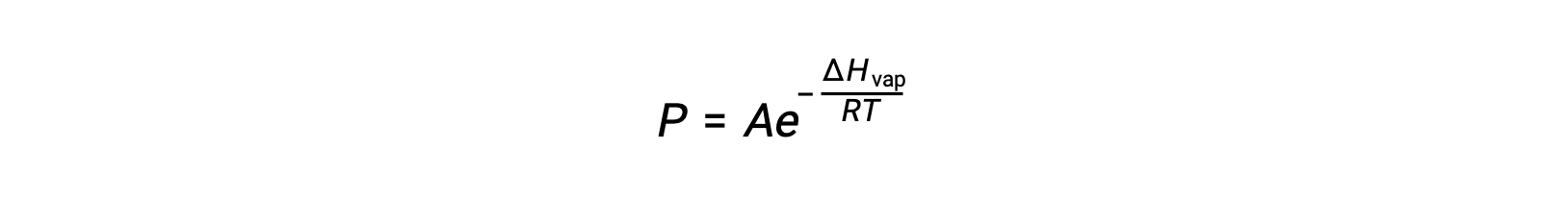
where ΔHvap is the enthalpy of vaporization for the liquid, R is the gas constant, and A is a constant whose value depends on the chemical identity of the substance. Temperature (T) must be in kelvin in this equation. However, since the relationship between vapor pressure and temperature is not linear, the equation is often rearranged into logarithmic form to yield the linear equation:
ΔHvap, sıvı için buharlaşma entalpisi, R, gaz sabiti ve A, değeri maddenin kimyasal kimliğine bağlı olan bir sabittir. Bu denklemde sıcaklık (T) kelvin cinsinden olmalıdır. Bununla birlikte, buhar basıncı ile sıcaklık arasındaki ilişki doğrusal olmadığından, doğrusal denklem elde etmek için denklem genellikle logaritmik formda yeniden düzenlenir:
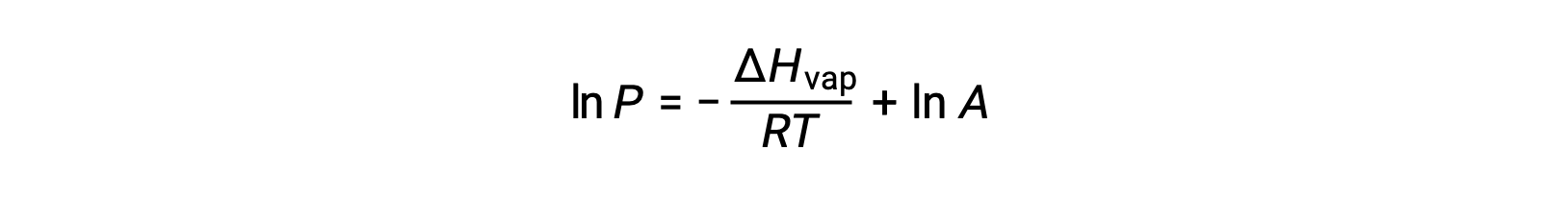
Herhangi bir sıvı için, belirli bir sıcaklıktaki buharlaşma entalpisi ve buhar basıncı biliniyorsa, Clausius-Clapeyron denklemi sıvının farklı bir sıcaklıktaki buhar basıncını belirlemeye izin verir. Bunu yapmak için doğrusal denklem iki noktalı bir formatta ifade edilebilir. T1 sıcaklığında, buhar basıncı P1 ise ve T2 sıcaklığında, buhar basıncı P2 ise, karşılık gelen doğrusal denklemler şunlardır:
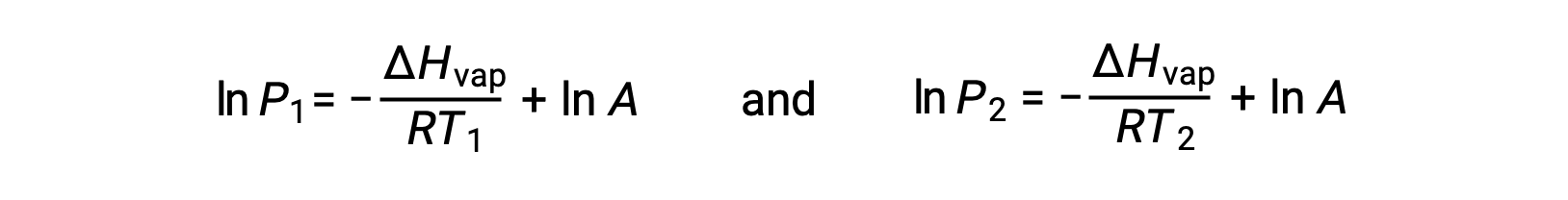
Since the constant, A, is the same, these two equations may be rearranged to isolate ln A and then set them equal to one another:
A sabiti aynı olduğundan, bu iki denklem lnA‘yı izole etmek ve sonra bunları birbirine eşitlemek için yeniden düzenlenebilir:
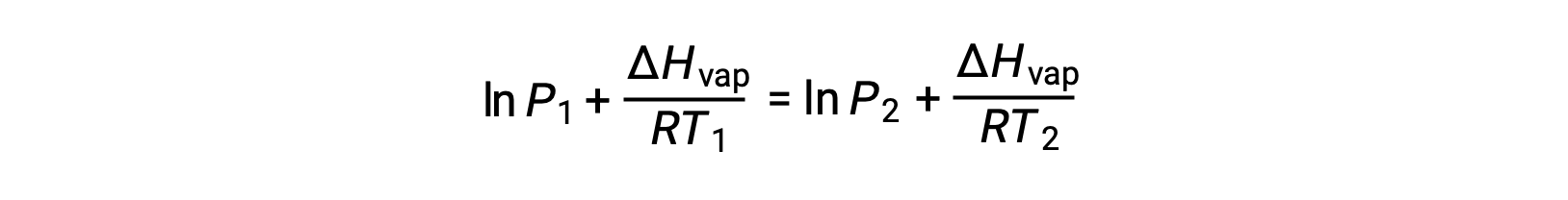
aşağıdakilerle birleştirilebilir:
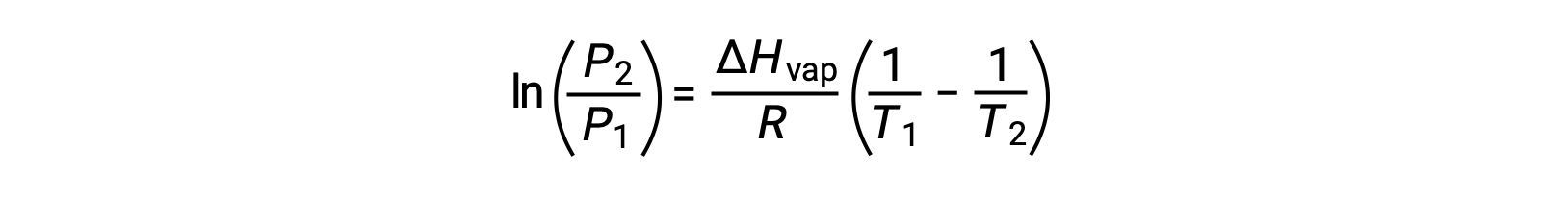
Bu metin bu kaynaktan uyarlanmıştır Openstax, Chemistry 2e, Section 10.3: Phase Transitions.
