13.5: 积分速率定律：浓度对时间的依赖
差分速率定律与反应物的速率和浓度有关，而速率定律的第二种形式称为综合速率法则，与反应物的浓度和时间有关。积分速率定律可用于确定一段时间后存在的反应物或生成物的数量，或估算某种反应在某种程度上进行所需的时间。 例如，积分速率定律有助于确定放射性物质必须存放多久才能使其放射性衰减到安全水平。
使用微积分，化学反应的差分速率定律可以结合时间来提供一个方程，将反应剂 / 产品数量与反应的经过时间相关。
一阶反应
通过集成速率定律进行简单的一阶反应 (率值 = k[A]) ，方程会随时间描述反应物浓度中的变化：
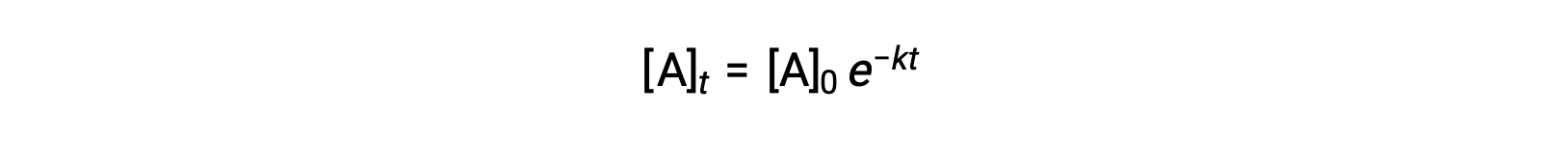
在这里，[A]t 是A任何时候的浓度 t ，[A]0 是的初始浓度， k 是第一个率值常量。 为了便于计算，此方程被重新排列为显示浓度对时间的线性依赖的格式，格式为直线方程 (y = mx + b):
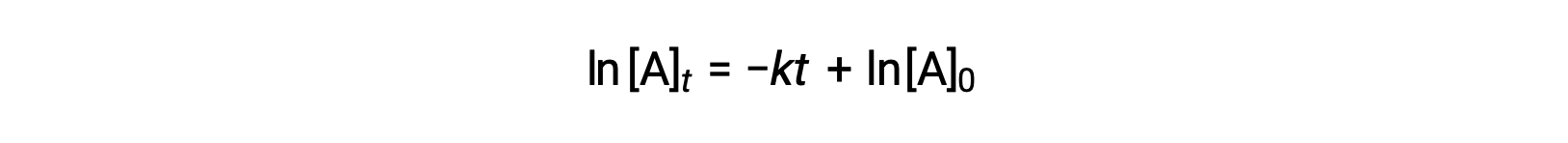
该等式表明，一阶ln [ A ] t 与 t 的关系图 反应是一条斜率为＆＃8722; k 且ln [ A ] 0 < / sub>。 如果以这种方式绘制一组速率数据但未得出直线，则该反应不是 A 中的一阶。
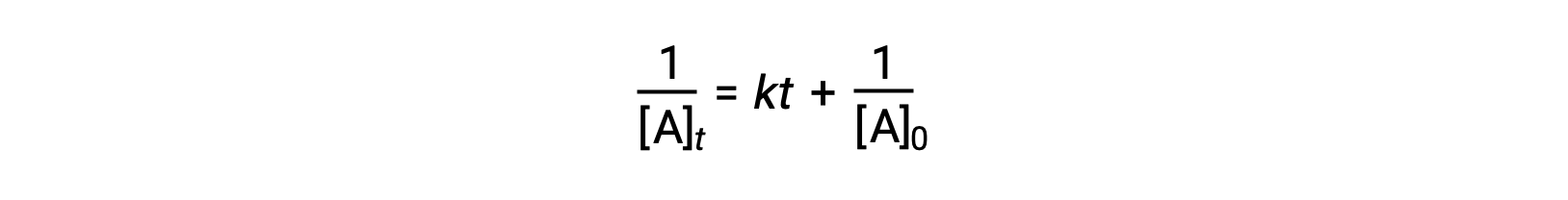
二阶反应 用于简单二阶反应的差分速率定律为率值 =k[A]2, 积分速率定律为： 二阶积分率定律也采用直线方程的形式。 根据等式，二阶反应的1 / [A] t 与 t 的图是一条直线，斜率为 k 和y截距1 / [A] 0 。 如果该图不是直线，则反应不是二阶的。
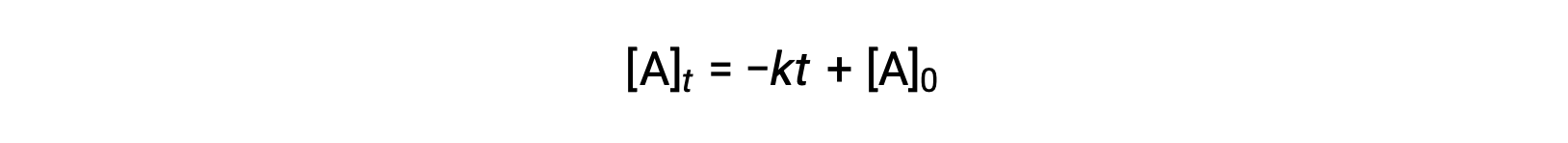
零阶反应 对于零阶反应，差分速率定律为率值 = K 零阶反应显示恒定反应率值，而不管其反应剂的浓度如何。 只有在特定条件下，才会观察到一些反应的零阶动力学。 当特定条件未得到满足时，这些相同的反应会表现出不同的动能行为，因此，有时会使用更谨慎的”伪零阶”术语。 零阶反应的积分速率定律也是一个线性函数，其形式为y = mx + b: 零级反应的[A]与时间 t 的关系图是一条直线，其斜率为＆＃8722; k 和 y -[ A ] 0 的截距。
