17.3:
Deuxième loi de la thermodynamique
17.3:
Deuxième loi de la thermodynamique
Dans le but d’identifier une propriété qui peut prévoir de manière fiable la spontanéité d’un processus, un candidat prometteur a été identifié : l’entropie. Les processus qui impliquent une augmentation de l’entropie du système (ΔS > 0) sont très souvent spontanés ; cependant, les exemples du contraire sont abondants. En élargissant la prise en compte des variations d’entropie pour inclure l’environnement extérieur, on peut arriver à une conclusion significative concernant la relation entre cette propriété et la spontanéité. Dans les modèles thermodynamiques, le système et l’environnement extérieur comprennent tout, c’est-à-dire l’univers, et donc ce qui suit est vrai :

Pour illustrer cette relation, envisagez à nouveau le processus de flux de chaleur entre deux objets, l’un identifié comme le système et l’autre comme l’environnement. Il existe trois possibilités pour un tel processus :
- Les objets sont à des températures différentes et la chaleur se propage de l’objet le plus chaud vers l’objet le plus froid. On observe toujours que cela se produit spontanément. En désignant l’objet le plus chaud comme étant le système et en invoquant la définition de l’entropie, cela donne les résultats suivants :
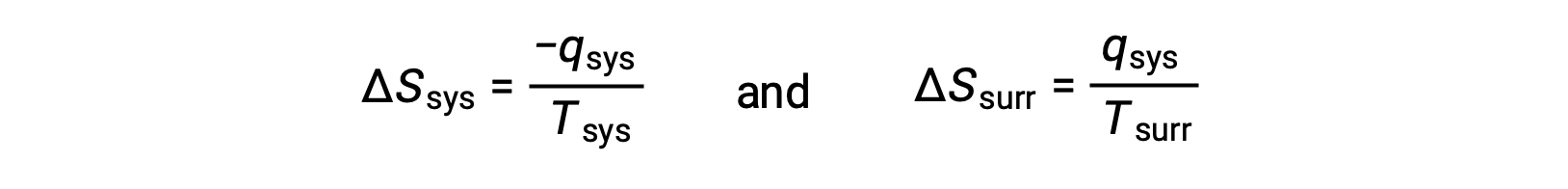
Les valeurs absolues de −qsys et qsys sont égales, leurs signes arithmétiques opposés indiquant la perte de chaleur par le système et le gain de chaleur par l’environnement extérieur. Puisque Tsys > Text dans ce scénario, la diminution de l’entropie du système sera inférieure à l’augmentation de l’entropie de l’environnement extérieur, et donc l’entropie de l’univers augmentera :
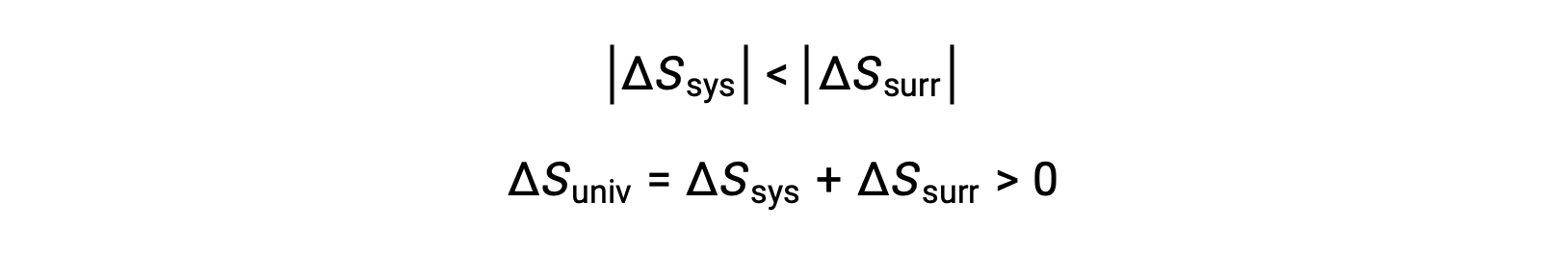
- Les objets sont à des températures différentes et la chaleur se propage de l’objet le plus froid vers l’objet le plus chaud. Cela n’est jamais observé spontanément. En désignant de nouveau l’objet le plus chaud comme étant le système et en invoquant la définition de l’entropie, on obtient ce qui suit :
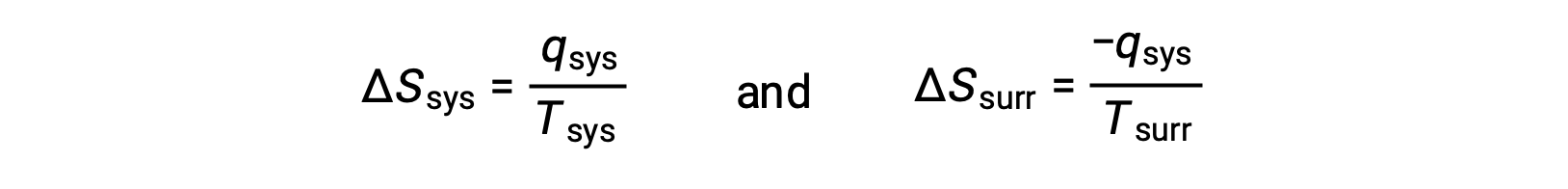
les signes arithmétiques de qsys indiquent le gain de chaleur par le système et la perte de chaleur par l’environnement extérieur. La valeur absolue de la variation d’entropie de l’environnement extérieur sera encore plus grande que celle du système, mais dans ce cas, les signes des variations de chaleur (c’est-à-dire la direction du flux de chaleur) donnera une valeur négative pour ΔSuniv. Ce processus implique une diminution de l’entropie de l’univers.
- Les objets sont essentiellement à la même température, Tsys ≈ Text, et donc les valeurs absolues des variations d’entropie sont essentiellement les mêmes pour le système et pour l’environnement. Dans ce cas, la variation d’entropie de l’univers est nulle et le système est à l’équilibre.
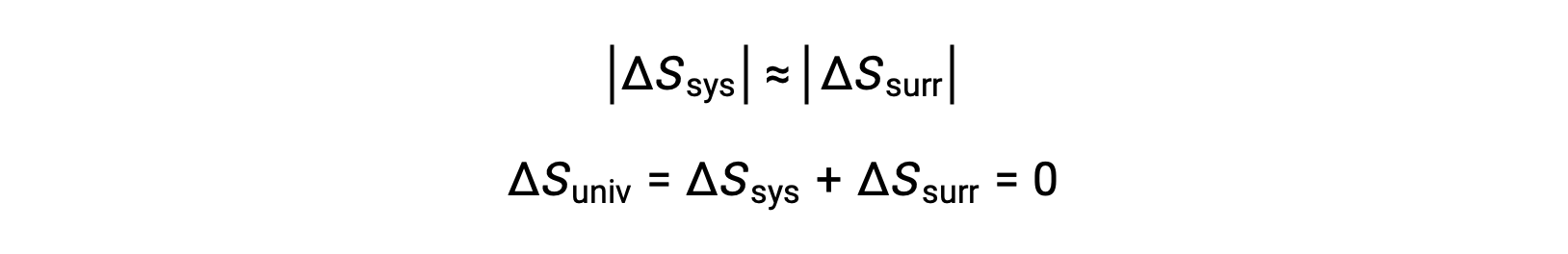
Ces résultats conduisent à une déclaration approfondie concernant la relation entre l’entropie et la spontanéité connue sous le nom du deuxième principe de la thermodynamique : tous les changements spontanés provoquent une augmentation de l’entropie de l’univers. Un résumé de ces trois relations est fourni dans le tableau ci-dessous.
| Le deuxième principe de la thermodynamique | |
| ΔSuniv > 0 | spontané |
| ΔSuniv < 0 | non spontané (spontané dans le sens opposé) |
| ΔSuniv = 0 | à l’équilibre |
Pour de nombreuses applications réalistes, l’environnement extérieur est vaste par rapport au système. Dans de tels cas, la chaleur gagnée ou perdue par l’environnement à la suite d’un processus représente une très petite fraction, presque infinitésimale, de son énergie thermique totale. Par exemple, la combustion d’un combustible dans l’air implique le transfert de chaleur d’un système (les molécules de combustible et d’oxygène qui subissent une réaction) vers un environnement extérieur infiniment plus grand (l’atmosphère terrestre). Par conséquent, qext est une bonne approximation de qsys, et le deuxième principe peut être indiqué comme suit :
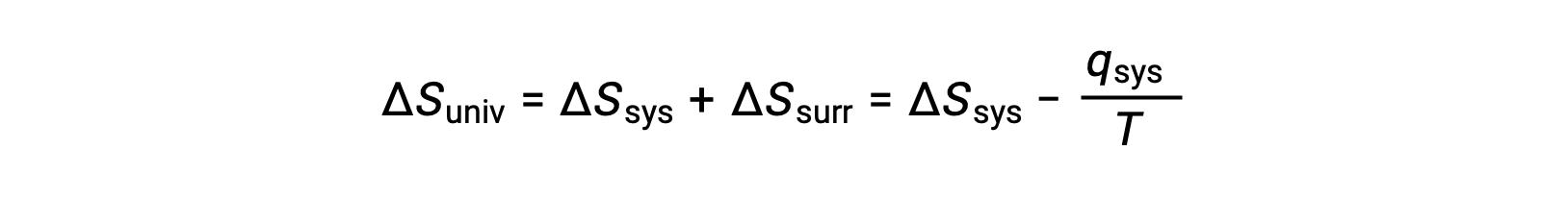
Cette équation est utile pour prévoir la spontanéité d’un processus.
Ce texte est adapté de Openstax, Chimie 2e, Chapitre 16.2 : Le deuxième et troisième principe de la thermodynamique.
