17.2: Entropy
Salt particles that have dissolved in water never spontaneously come back together in solution to reform solid particles. Moreover, a gas that has expanded in a vacuum remains dispersed and never spontaneously reassembles. The unidirectional nature of these phenomena is the result of a thermodynamic state function called entropy (S). Entropy is the measure of the extent to which the energy is dispersed throughout a system, or in other words, it is proportional to the degree of disorder of a thermodynamic system. The entropy may either increase (ΔS > 0, disorder increases) or decrease (ΔS < 0, disorder decreases) as a result of physical or chemical changes to the system. The change in entropy is the difference between the entropies of the final and initial states: ΔS = Sf - Si.
Boltzmann’s Theory of Microstates
A microstate is a specific configuration of all the locations and energies of the atoms or molecules that make up a system. The relation between a system’s entropy and the number of possible microstates (W) is S = k ln W, where k is the Boltzmann constant, 1.38 × 10−23 J/K.
The change in entropy is
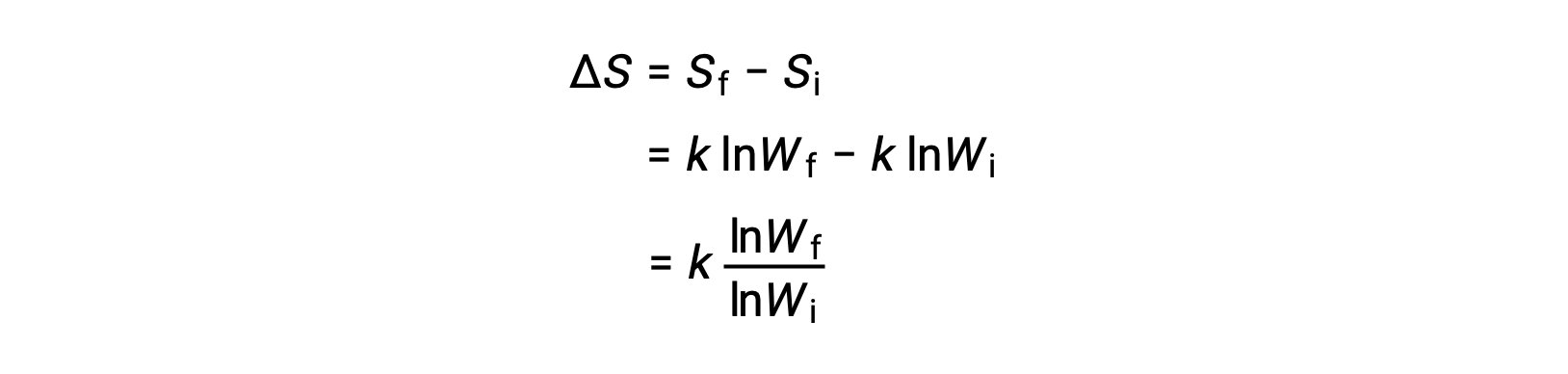
A system that has a greater number of possible microstates is more disordered (higher entropy) than an ordered system (lower entropy) with a fewer number of microstates. For processes involving an increase in the number of microstates, Wf > Wi, the entropy of the system increases and ΔS > 0. Conversely, processes that reduce the number of microstates, Wf < Wi, yield a decrease in system entropy, ΔS < 0.
Consider the distribution of an ideal gas between two connected flasks. Initially, the gas molecules are confined to just one of the two flasks. Opening the valve between the flasks increases the volume available to the gas molecules (energy is more dispersed through a larger domain) and, correspondingly, the number of microstates possible for the system. Since Wf > Wi, the expansion process involves an increase in entropy (ΔS > 0) and is spontaneous.
A similar approach may be used to describe the spontaneous flow of heat. A hot cup of tea evenly disperses its energy over a larger number of air particles in the cooler room, resulting in a larger number of microstates.
Generalizations Concerning Entropy
The relationships between entropy, microstates, and matter/energy dispersal allow generalizations to be made regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes.
In the solid phase, the atoms or molecules are restricted to nearly fixed positions with respect to each other and are capable of only modest oscillations about these positions. Thus, the number of microstates is relatively small. In the liquid phase, the atoms or molecules are free to move over and around each other, though they remain in relatively close proximity to one another. Thus, the number of microstates is correspondingly greater than for the solid. As a result, Sliquid > Ssolid and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, ΔS > 0. By the same logic, the reciprocal process (freezing) exhibits a decrease in entropy, ΔS < 0.
In the gaseous phase, a given number of atoms or molecules occupy a much greater volume than the liquid phase, corresponding to a much greater number of microstates. Consequently, for any substance, Sgas > Sliquid > Ssolid and the processes of vaporization and sublimation likewise involve increases in entropy, ΔS > 0. Likewise, the reciprocal phase transitions—condensation and deposition—involve decreases in entropy, ΔS < 0.
According to kinetic-molecular theory, the temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature of a substance will result in more extensive vibrations of the particles in solids and more rapid translations of the particles in liquids and gases. At higher temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also more dispersed than at lower temperatures. Thus, the entropy for any substance increases with temperature.
The entropy of a substance is influenced by the structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle’s mass and the spacing of quantized translational energy levels. For molecules, greater numbers of atoms increase the number of ways in which the molecules can vibrate and thus the number of possible microstates and the entropy of the system.
Finally, variations in the types of particles affect the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system composed of non-identical components. For example, when a solid dissolves in a liquid, the particles of the solid experience greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution, therefore, involves an increase in entropy, ΔS > 0.
This text is adapted from Openstax, Chemistry 2e, Chapter 16.2: Entropy.


