7.6:
Emission Spectra
When an atom absorbs energy, the electrons become excited and move to a higher energy level. As the electrons relax down to either a lower energy state or to the ground state, the excess energy is released as a photon.
The wavelength of the absorbed and emitted light depends on the difference between the high and low energy levels. High energy emitted light results from electrons relaxing from a higher energy level, and low energy emitted light results from electrons relaxing from a lower energy level.
An emission spectrum is a measure of emitted radiation across a range of wavelengths. With pure elemental species, the emission behavior appears as lines of specific wavelengths rather than a broad spectrum. This is the emission spectrum for hydrogen.
The set of spectral lines in the visible light region is known as the Balmer series. It occurs when electrons transition from an energy level higher than n = 3 back down to n = 2.
The visible light spectrum appears as spectral lines at 410, 434, 486, and 656 nm, which correspond to energy level transitions from n = 3, 4, 5, and 6, respectively, to n = 2. Additional spectral lines can be measured outside of the visible range, such as the Lyman series in the UV region and the Paschen series in the infrared region.
The wavelengths of spectral lines for hydrogen can be predicted using a mathematical expression, where RH is the Rydberg constant, n1 is the principal quantum number of the lower energy level, and n2 is the principal quantum number for the higher energy level. For the Balmer series, n1 = 2.
Since different atoms have different energy levels, the spectral emission lines vary from element to element and are used to identify substances.
The inverse of an emission spectrum is its absorption spectrum. Looking at hydrogen, the lines in its absorption spectrum are located at the same wavelengths of its emission spectrum, but they are dark. These are the wavelengths of light that are absorbed by a hydrogen atom when it is exposed to a continuous white light spectrum.
7.6:
Emission Spectra
When solids, liquids, or condensed gases are heated sufficiently, they radiate some of the excess energy as light. Photons produced in this manner have a range of energies, and thereby produce a continuous spectrum in which an unbroken series of wavelengths is present.
In contrast to continuous spectra, light can also occur as discrete or line spectra having very narrow linewidths interspersed throughout the spectral regions. Exciting a gas at low partial pressure using an electrical current, or heating it, will produce line spectra. Fluorescent light bulbs and neon signs operate in this way. Each element displays its own characteristic set of lines, as do molecules, although their spectra are generally much more complicated.
Each emission line consists of a single wavelength of light, which implies that the light emitted by a gas consists of a set of discrete energies. For example, when an electric discharge passes through a tube containing hydrogen gas at low pressure, the H2 molecules are broken apart into separate H atoms and a blue-pink color is observed. Passing the light through a prism produces a line spectrum, indicating that this light is composed of photons of four visible wavelengths.
The origin of discrete spectra in atoms and molecules was extremely puzzling to scientists in the late nineteenth century. According to classical electromagnetic theory, only continuous spectra should be observed. Other discrete lines for the hydrogen atom were found in the UV and IR regions. Johannes Rydberg generalized Balmer's work and developed an empirical formula that predicted all of hydrogen's emission lines, not just those restricted to the visible range, where, n1 and n2 are integers, n1 < n2
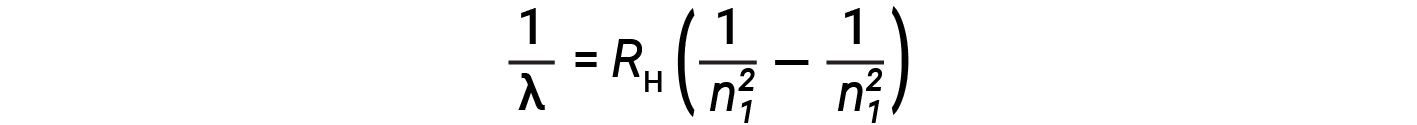
Even in the late nineteenth century, spectroscopy was a very precise science, and so the wavelengths of hydrogen were measured to very high accuracy, which implied that the Rydberg constant could be determined very precisely as well. That such a simple formula as the Rydberg formula could account for such precise measurements seemed astounding at the time, but it was the eventual explanation for emission spectra by Neils Bohr in 1913 that ultimately convinced scientists to abandon classical physics and spurred the development of modern quantum mechanics.
This text is adapted from Openstax, Chemistry 2e, Section 3.1: Electromagnetic Energy.
