Overview
Source: Ketron Mitchell-Wynne, PhD, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
This experiment demonstrates the kinematics of motion in 1 and 2 dimensions. This lab will begin by studying motion in 1 dimension, under constant acceleration, by launching a projectile directly upward and measuring the maximum height reached. This lab will verify that the maximum height reached is consistent with the kinematic equations derived below.
Motion in 2 dimensions will be demonstrated by launching the ball at an angle θ. Using the kinematic equations below, one can predict the distance to where the projectile will land based upon the initial speed, total time, and angle of trajectory. This will demonstrate kinematic motion with and with out acceleration in the y- and x-directions, respectively.
Principles
Any measurement of the kinematics of an object, such as position, displacement, and speed, must be made with respect to some reference frame. The x-direction of the coordinate axes will correspond to the horizontal direction, and y to the vertical. The origin of the coordinate axes (0, 0), will be defined as the initial position of the particle (here, a ball).
Motion in 1 dimension
Let's begin by considering the 1-dimensional motion of a ball over some particular time interval t, corresponding to position y. Denote the initial time as t0, which corresponds to position y0. The displacement of the ball, Δy, is defined as:
Δy = y - y0. (Equation 1)
The average velocity of the ball, v-, is the displacement divided by the elapsed time:
v-= (y - y0)/(t - t0) = Δx/Δt.(Equation 2)
The instantaneous velocity, v, is the velocity over some very small time interval, defined as:
v = limΔt→→ 0 (Δx/Δt). (Equation 3)
The constant acceleration, a, is the change in velocity divided by the elapsed time:
a = (v - v0)/(t - t0). (Equation 4)
Set t0 = 0 to be the initial time and solve for v in the last equation to obtain the velocity as a function of time:
v = v0 + at.(Equation 5)
Next, calculate the position y as a function of time using Equation 2. y is re-labelled as:
y = y0 + v-t. (Equation 6)
Under constant acceleration, the velocity will increase at uniform rate, so the average velocity will be halfway between the initial and final velocities:
v- = (v0 + v)/2. (Equation 7)
Substituting this into Equation 6 and using the definition of instantaneous velocity gives a new equation for y:
y = y0 + v0t + ½ at2.(Equation 8)
t is solved for by substituting Equation 7 into Equation 6:
t = (v - v0)/a. (Equation 9)
Substituting that t into Equation 6 and again using the definition of Equation 7 again changes the equation for y:
y = y0 + (v + v0)/2 (v - v0)/a = y0 + (v2 - v02)/2a. (Equation 10)
Solving for v2 gives:
v2 = v02 + 2a(y - y0). (Equation 11)
These are the useful equations relating position, velocity, acceleration, and time when a is constant.
Motion in 2 dimensions
Now, motion in 2 dimensions will be considered. Equations 5, 7, 8,and 11 constitute a general set of kinematic equations in the y-direction. These can be expanded to motion in 2 dimensions, x and y, by simply replacing the y components with x components. Consider a projectile launched with an initial velocity v0at an angle θ with respect to the x-axis, as shown in Figure 1. From the figure, one can see that the x-direction component for the initial velocity, vx,0, is v0cos(θ). Similarly, in the y-direction, vy,0 = v0sin(θ).
The only acceleration the particle experiences is gravity in the negative y-direction. Therefore, the velocity in the x-direction is constant. The velocity in the y-direction reaches a minimum at the peak of the parabola, halfway through the displacement, at t/2, where t is the total time. Use the equations above to describe this 2-dimensional motion with equations. In this coordinate frame, the origin (0,0) corresponds to (x0, y0). Starting with the x-direction
x = x0 + vx,0 t + ½ axt2 (Equation 12)
= v0 cos(θ)t. (Equation 13)
In the y-direction
y = y0 + vy,0t + ½ ay t2 (Equation 14)
= v0sin(θ)t - ½ g t2,(Equation 15)
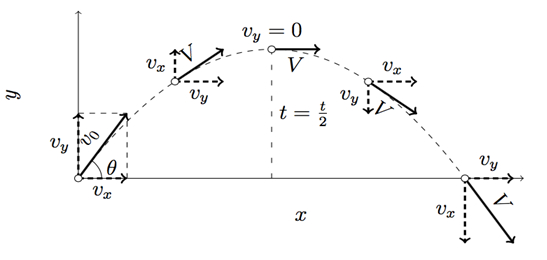
Figure 1. Projectile motion in 2 dimensions. A projectile is launched with initial velocity v0at an angle θ with respect to the x-axis. The two velocity components are vxand vy, where V = vx +vy.
where g is the gravitational acceleration. If one measures the time it takes for the projectile to complete its path and the angle θ and the initial velocity v0 are known, the displacement in the x- and y-directions can be calculated. Before beginning this experiment, the muzzle velocity of the launcher, 6.3 m/s, is known.These displacement calculations will be compared to the experimental results. A similar procedure can be done in 1 dimension by shooting the projectile directly upwards, with θ = 0.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Motion in 1 dimension.
- Obtain a ball, a launcher with a plunger, two poles, a bucket, two clamps, a bungee cord, and a 2-m stick.
- Attach the launcher to a pole, with a 2-m length of pole above it.
- Use the plunger to place the ball in the launcher at maximum spring tension.
- Angle the launcher directly upwards so θ = 0.
- Launch the ball and use a stopwatch to measure the total time t it takes the ball to reach its maximum height. The initial position is where the ball exits the launcher.
- Notice that the ball reaches a maximum height of 2 meters and stopsinstantaneously when it reaches that height.
- Repeat steps 1.5-1.6 five times and use the average time for calculations.
2. Motion in 2 dimensions.
- Set the launcher and the other pole 4 m apart, at the same horizontal height. Attach the bucket to the other pole using the clamp and bungee cord (Figure 2). The height of the bucket should be the same as the height at whichthe ball exits the launcher.
- Use the plunger to place the ball in the launcher at maximum spring tension.
- Angle the launcher at a 45° angle so θ = π/4.
- Use a stopwatch to measure the total time t it takes the ball to land in the bucket.
- Take note of the approximate height the ball reaches.
- Repeat steps 2.4-2.5 five times and use the average time for calculations.

Figure 2. Experimental setup.
Kinematics is the description of motion, which is often an important consequence of many physical events and phenomena.
Motion can be one-dimensional, two-dimensional, or three-dimensional. The equations that apply to an object's movement in all these cases use the vector quantities of position - which is displacement with respect to origin, velocity - which is change in position with time, and acceleration-which is change in velocity with time.
With this information, it is possible to calculate the paths of free falling bodies, the trajectories of projectiles, and the orbits of planets, to give only a few examples.
Here, we will focus on kinematical equations related to the one-dimensional rise and fall of an object and the two-dimensional arc of an object launched at an angle
Before describing motion, it is necessary to have a coordinate system, or a frame of reference. Typically, the x-axis is horizontal and the y-axis is vertical. The origin is arbitrary but is often an object's starting point.
Let's consider a basketball placed at the origin and thrown straight up. The ball's position is its distance and direction from the origin and has units of meters.
Average velocity vy is the change of position Δy divided by the change in time Δt, and has units of meters per second. However, as Δt approaches zero, the average velocity equation becomes one for instantaneous velocity .
Practically, think of instantaneous velocity as the velocity in that instant. So at start the instantaneous velocity v0 is the launching velocity, and following that the instantaneous velocity decreases continuously until it is zero at the peak.
The decrease in velocity due to constant acceleration provided by Earth's gravity, which opposes the ball's motion and is negative in this coordinate system.
In such constant acceleration conditions, the kinematical relationships lead to these equations for the magnitude of instantaneous velocity and position in one dimension. Using them, we can calculate an object's motion at any given time
Let's apply these formulae to the basketball example. Let's say that the basketball's launching velocity, v0, is 20 meters per second. We know that the ball's final instantaneous velocity at the peak is zero. The acceleration here is negative g, since it opposes the ball's motion. Thus, by rearranging this kinematics equation, we can obtain t -- the rise time, which comes out to be approximately two seconds. Now, using the kinematic formula for position, and saying that the initial position y0 is zero, we can plug in the values for launch velocity acceleration due to gravity and rise time, to calculate the maximum displacement, which is the peak height here, of approximately 20.4 meters. After reaching the peak, the ball falls for two seconds with increasing velocity until it hits the ground where it started, making the total flight time to be approximately 4 seconds.
For two dimensions, an object's vertical and horizontal motions are independent of each other and can be treated separately, with the net result being the vector sum. Using this insight, the entire arc of projectile motion may be decomposed into two separate, one-dimensional motions.
Let's study this using an example: a pitcher throws a baseball with an initial speed of 20 meters/second at an angle of thirty degrees from the ground. The initial vertical component of velocity is this speed times the sine of 30 degrees, or 10 meters/second. The initial horizontal component is the speed times the cosine of 30 degrees, or about 17 meters/second.
During the baseball's rise time, the vertical velocity is upward with speed decreasing due to gravity. At the peak, which is the mid-point, the vertical velocity is zero for an instant. Then during the fall time, it is downward with increasing speed.
Ignoring air resistance, horizontal motion has no acceleration and therefore has constant velocity.
Vector addition of vertical and horizontal positions and vertical and horizontal velocities produces the arc of projectile motion. The sum of the rise and fall times is the total flight time, which determines the range, or the horizontal distance.
Now that we've seen how to calculate the paths of moving objects, we will test the kinematical equations on a ball thrown straight upward and one thrown at an angle.
These experiments use a ball, a launcher with plunger, two poles, a bucket, two clamps, and a two-meter long stick and a stopwatch. Note that the muzzle velocity of the launcher is 6.3 meters per second. For the first experiment, which demonstrates one-dimensional projectile motion, attach the launcher to a pole and position the two-meter stick above it.
Adjust the launcher so it is pointed directly upwards at an angle of zero degrees from the vertical. This corresponds to a launch angle of 90 degrees from the horizontal. Note the vertical position of the tip of the launcher, where the ball will exit, and designate it y0.Use the plunger to place the ball in the launcher at maximum spring tension.
Launch the ball and start a stopwatch at the same instant. Measure the total time for the ball to return to its starting point at vertical position y0 and record the result as flight time. Notice the ball reaches a maximum height of approximately 2 meters and stops for an instant at this point.
Repeat this procedure five times and use the average total time for later calculations.
This second experiment demonstrates two-dimensional projectile motion. Set up the launcher as in the first experiment and place the other pole four meters away at the same height. Attach the bucket to this second pole with the clamp and adjust the bucket so it is at the same height as the tip of the launcher.
Attach the 2-meter stick in the middle of the configuration, and position it so there is at least one meter above the height of the launcher, or y0. Adjust the launcher so it is at a 45-degree angle from the vertical, which is a launch angle of 45 degrees from the horizontal. Use the plunger to place the ball in the launcher at maximum spring tension.
Now launch the ball and start the stopwatch at the same instant. Measure the total flight time for the ball to land in the bucket. Note and record the maximum height the ball reaches. Repeat this experiment five times and use the average total time for later calculations.
For the experiment demonstrating motion in one dimension, the initial velocity of the ball out of the launch mechanism was 6.3 meters per second. Recall, when a ball is thrown straight up, its velocity is 0 at the peak. With this information and the kinematics formula for velocity, we can calculate the ball's theoretical rise time to be 0.64 seconds. Multiplying this by 2 gives us the calculated flight time. Then, using the formula for position, we can calculate the peak height to be 2.02 meters.
The theoretical and measured results are comparable, within experimental error, validating the kinematics equations for one-dimensional motion
For the experiment demonstrating motion in two dimensions, the ball was launched with a speed of 6.3 meters/second at a 45-degree angle. To calculate its projectile motion, first determine the x-component of the initial velocity-v•cosθ-and the y component of the initial velocity-v•sinθ. Then use the initial vertical velocity and acceleration to determine the time to reach peak height, which comes out to be 0.45 seconds. Therefore, the total flight time is double this value, or 0.9 seconds.
To calculate the maximum vertical displacement, use the initial vertical velocity, the acceleration due to gravity, and the rise time. This gives us the theoretical maximum y displacement of 1 meter. To calculate the maximum horizontal displacement, use the initial horizontal velocity and total flight time, which results in theoretical maximum x displacement of 4 meters.
Again, theory agrees well with the experiment, validating the kinematics equations for two-dimensional motion.
The use of kinematics and the understanding of projectile motion are important, and often invisible, in many everyday applications.
Automobile engineers often use kinematics to calculate different car specifications.
One of them is the stopping or braking distance, which is an important safety parameter that can be computed using one-dimensional kinematics equations
Without knowing it, a golfer performs mental calculations using kinematics with every swing of the club. Hoping for a hole-in-one, the golfer swings, strikes the ball and launches it with a certain speed and angle to fly across the course. The golf ball's ideal two-dimensional path obeys the equations governing projectile motion.
You've just watched JoVE's introduction to kinematics and projectile motion. You should now know how to use kinematic equations to calculate the trajectory of an object moving in one or two dimensions. As always, thanks for watching!
Subscription Required. Please recommend JoVE to your librarian.
Results
Representative results from steps 1 and 2 of the above procedure are listed below in Table 1. This table records the maximum height the ball reached in both 1 and 2 dimensions, with a known initial velocity and total flight time. The value of the experimentally measured maximum vertical displacement is compared to that calculated using Equation 15, the value of which is also found below. The table also records the maximum horizontal displacement of the ball for the 2-dimensional experiment. This is compared with the calculated value from Equation 13 using the known initial velocity and measured flight time. These two results match very well, which validates the kinematic equations.
| Calculated Flight Time (s) | Calculated y (m) | Average Measured Flight time (s) | Average Measured y (m) |
| 1.28 | 2.02 | 1.22 | 2.1 |
Table 1. Calculated and measured results in one dimension.
| Calculated Flight Time (s) | Calculated y (m) | Calculated x (m) | Average Measured Flight time (s) | Average Measured y (m) | Average Measured x (m) |
| 0.9 | 1.01 | 4.01 | 1.02 | 1.1 | 4 |
Table 2. Calculated and measured results in two dimensions.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
Kinematics is used in a wide range of applications. The military uses these kinematic equations to determine the best way to launch ballistics. For better accuracy, the drag of air resistance is included in the equations. Car manufactures use kinematics to figure out top speeds and stopping distances. In order to take off,airplanes must attain a certain speed before they run out of runway. With kinematics,it is possible compute how fast the pilot will need to accelerate when taking off at a certain airport.
Subscription Required. Please recommend JoVE to your librarian.




