Overview
Source: Tamara M. Powers, Department of Chemistry, Texas A&M University
Metal carbonyl complexes are used as metal precursors for the synthesis of organometallic complexes as well as catalysts. Infrared (IR) spectroscopy is one of the most utilized and informative characterization methods of CO containing compounds. Group theory, or the use of mathematics to describe the symmetry of a molecule, provides a method to predict the number of IR active C-O vibrational modes within a molecule. Experimentally observing the number of C-O stretches in the IR is a direct method to establish the geometry and structure of the metal carbonyl complex.
In this video, we will synthesize the molybdenum carbonyl complex Mo(CO)4[P(OPh)3]2, which can exist in the cis- and trans-forms (Figure 1). We will use group theory and IR spectroscopy to determine which isomer is isolated.
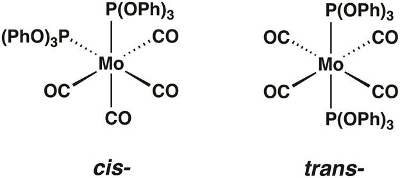
Figure 1. The cis- and trans-isomers of Mo(CO)4[P(OPh)3]2.
Principles
Selection Rules:
Selection rules dictate the number of electronic transitions, from one quantum state to another, that are possible for a given molecule. IR spectroscopy probes vibrational transitions from the molecule's ground state, v = 0, to the first excited state, v = 1. The number of degrees of vibrational freedom (normal modes of vibration) for linear and non-linear molecules can be calculated using Equation 1 and Equation 2, respectively.
3N - 5 (1)
3N - 6 (2)
where N = the number of atoms in the molecule
For a normal mode of vibration to be IR active, the molecule's dipole must change. Therefore, any normal modes of vibration where a change in dipole does not occur are IR inactive. The number of active IR modes can be determined using group theory.
Group Theory:
Chemists use group theory to understand the relationship between the symmetry and physical properties of a molecule. While the scope of group theory is too broad to rigorously cover in this video, we will provide the necessary tools needed to apply group theory to simple coordination complexes and show how it can be used to predict the number of IR active vibrational modes. To demonstrate, we will walk through the application of group theory to the molecule cis-Mo(CO)4[P(OPh)3]2.
First, we need to determine the point group of the molecule. Point groups are used to describe the symmetry elements present in a given molecule. To determine the point group of cis-Mo(CO)4[P(OPh)3]2, we can use a flow chart called a symmetry tree, which asks a series of questions about the symmetry elements present in the molecule (Figure 2). Table 1 summarizes all of the symmetry elements included in the symmetry tree. Using the symmetry tree, and assuming that the ligands P(OPh)3 are point ligands (while ignoring the symmetry of those ligands), we find that cis-Mo(CO)4[P(OPh)3]2 is in the point group C2v.

Figure 2. Symmetry tree used for point group determination.
Table 1. Symmetry elements used in point group determination.
| Symmetry element | Symbol used | Example* |
| Identity | E |  |
| Rotation axis (rotation by 360°/n) |
Cn |  |
| Horizontal mirror plane (reflection about xy plane) |
σh |  |
| Vertical mirror plane (reflection about xz or yz plane) |
σv |  |
| Diagonal mirror plane (reflection between xz and yz planes) |
σd |  |
| Inversion Center | i |  |
| Improper rotation axis (rotation by 360°/n followed by reflection perpendicular to rotation axis) |
Sn |  |
| *Examples are for an octahedral complex, where ligands 1–6 are equivalent. Upon performing the operation, the resulting molecule should be indistinguishable from its original configuration. | ||
For the next step, we need to introduce character tables, which describe all of the symmetry present within a given point group. The character table for the point group C2v is shown below.
| C2v | E | C2 | σv(xz) | σv’(yz) | ||
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
The point group is indicated in the top left-hand corner of the character table. To the right of the point group, all of the symmetry operations inherent to that point group are listed. The subsequent rows list all of the symmetry representations (irreducible representations, represented by Mulliken symbols, i.e.,A1) contained in that point group, along with the symmetry of functions, which can tell us about the symmetry of atomic orbitals as well as linear movement along the x-, y-, and z-axis.
Using the character table for the point group C2v, we generate a reducible representation (Γred) of the C-O stretching modes in the molecule cis-Mo(CO)4[P(OPh)3]2 (Figure 3). The reducible representation, or the linear combination of irreducible representations, can be generated by applying each of the symmetry operations within the character table to the vibrations within molecule and recording the number of C-O vibrations that remain unchanged (in the same position in space). For example, upon applying the identity symmetry element to the C-O vibrations in cis-Mo(CO)4[P(OPh)3]2, all four of the vibrational arrows remain in the same position. Therefore, the first value in our reducible representation is 4. If we continue this exercise, we generate the reducible representation shown below.
| C2v | E | C2 | σv(xz) | σv’(yz) |
| Γred | 4 | 0 | 2 | 2 |
Next, we use the C2v character table to find the linear combination of irreducible representations that generates Γred for the C-O vibrations within cis-Mo(CO)4[P(OPh)3]2. Reduction of the reducible representation can be achieved using the reduction formula shown in Equation 3.
 (3)
(3)
where:
ni = number of times the irreducible representation i occurs in the reducible representation
h = order of the group (total number of symmetry operations)
c = the class of operation
gc = number of operations in the class
χi = character of the irreducible representation for the operations of the class
χr = character of the reducible representation for the operations of the class
Using Equation 3 for each of the irreducible representations in the character table C2v, we find that Γred = 2A1 + B1 + B2. All three of the contributing irreducible representations, A1, B1, and B2, are IR active because they transform as either the x-, y-, or z-axis (see the symmetry of functions in the character table). Therefore, we predict that cis-Mo(CO)4[P(OPh)3]2 will exhibit 4 C-O stretching modes in its IR spectrum.
To summarize, the following steps are needed in order to determine the number of IR active vibrational modes in a molecule:
1. Determine the point group of the molecule.
2. Generate a reducible representation of the C-O stretching vibrations within the molecule.
3. Reduce the reducible representation using Equation 3.
4. Identify the number of translational irreducible representations present in the reduced representation from step 3.
If we follow these 4 steps with trans-Mo(CO)4[P(OPh)3]2, we find that the molecule only possesses 1 active C-O vibrational mode.

Figure 3. CO vibrational stretches in cis-Mo(CO)4[P(OPh)3]2.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Setup of the Schlenk Line (for a more detailed procedure, please review the "Schlenk Lines Transfer of Solvent" video in the Essentials of Organic Chemistry series). Schlenk line safety should be reviewed prior to conducting this experiment. Glassware should be inspected for star cracks before use. Care should be taken to ensure that O2 is not condensed in the Schlenk line trap if using liquid N2. At liquid N2 temperature, O2 condenses and is explosive in the presence of organic solvents. If it is suspected that O2 has been condensed or a blue liquid is observed in the cold trap, leave the trap cold under dynamic vacuum. Do NOT remove the liquid N2 trap or turn off the vacuum pump. Over time the liquid O2 will sublime into the pump; it is only safe to remove the liquid N2 trap once all of the O2 has sublimed.
- Close the pressure release valve.
- Turn on the N2 gas and the vacuum pump.
- As the Schlenk line vacuum reaches its minimum pressure, prepare the cold trap with either liquid N2 or dry ice/acetone.
- Assemble the cold trap.
2. Synthesis of Mo(CO)4[P(OPh)3]2 (Figure 4)1
Note: Use standard Schlenk line techniques for the synthesis of Mo(CO)4[P(OPh)3]2 (see the "Synthesis of a Ti(III) Metallocene Using Schlenk line Technique" video). Metal carbonyl complexes are a source of free CO, which is highly toxic. Carbon monoxide poisoning occurs when CO binds to hemoglobin, resulting in significant reduction of oxygen supply to the body. Therefore, it is extremely important to take appropriate safety measures when handling and working with metal carbonyl complexes. Reactions that generate free CO need to be conducted in a well-ventilated hood to prevent exposure to the toxic gas.
- Add 1.6 g (4.92 mmol) Mo(CO)4(nbd) (nbd = 2,5-Norbornadiene) and 1.6 mL (9.84 mmol) triphenyl phosphite (P(OPh)3) to a 100 mL Schlenk flask and prepare the Schlenk flask for the cannula transfer of solvent.
Note: Mo(CO)4(nbd) ((Bicyclo[2.2.1]hepta-2,5-diene)tetracarbonylmolybdenum(0)) can be purchased from Sigma Aldrich or synthesized using literature methods.2 - Add 20 mL of degassed dichloromethane to the Schlenk flask via cannula transfer.
- Stir the reaction mixture for 4 h at room temperature under N2.
- Remove the volatiles under vacuum and wash the resulting precipitate with cold hexanes (two washes each with 10 mL, −78 °C).
- Dry the solid product under vacuum for 15 min.
- Measure the IR spectrum of the product in a solution of hexanes.

Figure 4. Synthesis of Mo(CO)4[P(OPh)3]2.
Group theory is a mathematical model connecting molecular symmetry to properties such as IR-active vibrational modes.
Every molecule can be classified with a point group, which describes every symmetry element present in a molecule with respect to a fixed point.
Group theory provides special tables, called character tables, to predict the effect of a molecule's symmetry on its vibrational modes and other important properties.
This video will discuss the underlying principles of group theory, illustrate the procedure for the synthesis and characterization of an isomer of Mo(CO)4[P(OPh)3]2, and introduce a few applications of group theory in chemistry.
Molecular symmetry describes the indistinguishable configurations of a molecule. The transformations between them are called symmetry operations, which occur with respect to one or more symmetry elements.
The five symmetry elements are proper and improper rotation axes, mirror planes, centers of inversion, and identity. Every molecule has the identity element, or E, in which no change occurs.
A mirror plane, labeled σ, is a reflection plane with identical starting and ending configurations. Molecules may have more than one mirror plane. A center of inversion, labeled i, is a point through which every atom is reflected.
A proper rotation axis is an axis around which a molecule rotates to an identical configuration. It is labeled Cn, where n is 360 divided by the angle of rotation.
An improper rotation axis, labeled Sn, is the axis around which a molecule is rotated and then reflected through a perpendicular mirror plane. Molecules may have more than one rotation axis. The axis with the highest n is the principal axis.
Molecules are assigned to point groups using a symmetry tree, which identifies the symmetry operations needed to classify the molecule.
For example, BF3 is non-linear. It does not have at least two axes with n greater than 2. It has at least one rotation axis; its principal axis is C3. It has three C2 axes perpendicular to its principal axis, and a mirror plane perpendicular to its principal axis. Thus, boron trifluoride belongs to the D3h point group.
Each point group has a character table listing its essential symmetry operations. Each row contains an irreducible representation of the operations, along with the corresponding atomic orbitals and linear movements.
Reducible representations are generated by evaluating how these symmetry operations affect molecular properties. Reducing this representation gives the contributing irreducible representations.
Now that you understand the principles of group theory, let's go through a procedure for synthesizing an isomer of Mo(CO)4[P(OPh)3]2 and comparing its IR spectrum to the number of IR-active modes predicted for each isomer by group theory.
To begin the procedure, close the Schlenk line vent, and start the flow of N2 gas. Turn on the vacuum pump and with the system at its minimum pressure, cool the vacuum trap with dry ice in acetone.
In a fume hood, measure out 0.5 g of Mo(CO)4(nbd) and place the molybdenum precursor into a 200-mL Schlenk flask. Equip the reaction flask with a stir bar and stopper the flask with a glass stopper. Connect the flask to the Schlenk line via the side arm, and prepare the flask for cannula transfer by evacuating the vessel for 5 minutes, followed by refilling the flask with N2. Repeat this evacuation and refill process a total of 3 times.
Next, prepare another Schlenk flask fitted with a rubber septum containing 20 mL of CH2Cl2. Connect the flask to the Schlenk line and secure the flask in the hood. Using a syringe, draw up 0.87 mL of triphenyl phosphite and dispense it into the Schlenk flask. Make sure the Schlenk line stopcock is open to N2. Degas the CH2Cl2/triphenyl phosphite mixture by bubbling N2 through the solvent for 10 minutes. Then use cannula transfer to add the solution to the flask containing the solid. Open the reaction flask to N2 gas and stir the mixture at room temperature for 4 hours.
Once the reaction has finished, replace the rubber septum with a glass stopper, and remove volatile solvents under vacuum.
Add hexanes to the resulting product and cool in a dry ice/acetone bath briefly, until a precipitate forms. Filter the precipitate and wash the precipitate twice with 10 mL of cold hexanes and collect the solid by filtration. Dry the solid product under vacuum for 15 minutes.
Lastly, dissolve a portion of the product in hexanes and load the solution into an IR cell. Acquire an IR spectrum of the complex.
Now, let's determine whether the product is the cis or trans isomer by assigning point groups to both isomers and comparing the predicted IR-active modes to the IR spectrum.
Neither the cis nor trans isomer is linear, and neither has more than two rotation axes with orders higher than 2. Both have at least one rotation axis. The principal axes for the cis and trans isomers are C2 and C4, respectively.
The cis isomer does not have two C2 axes perpendicular to its C2 axis, nor does it have a perpendicular mirror plane. It has two mirror planes containing the C2 axis, so its point group is C2v. The trans isomer has four C2 axes and a mirror plane perpendicular to its C4 axis, so its point group is D4h.
Next, reducible representations of the CO stretches are generated by applying each symmetry operation to the molecule and counting the C-O stretches that do not change locations in space.
The C2v table has four operations: identity, C2 rotation, and reflections through two mirror planes containing the C2 axis. In the identity operation, all four dipole moments remain in place. All four dipole moments take different positions after a C2 rotation. Two dipole moments remain in the same position for each reflection.
The reduction formula calculates the coefficient of each irreducible representation in the reducible representation. The point group order is the number of symmetry operations. Classes are types of symmetry operations. Here, the number of operations in each class is 1, which is traditionally omitted from a character table.
The character is the value corresponding to a representation for a given class. When the reduction formula is applied, three irreducible representations are found, with one occurring twice. These representations transform as either the x, y, or z axis, which is consistent with four IR-active C-O stretches.
Using the same technique, the trans isomer is found to have one IR-active C-O stretch. The IR spectrum of the molybdenum product has peaks at 2046, 1958, and 1942 cm-1. With higher resolution data, a fourth C-O stretch may be observed. Based on the obtained IR, one can conclude that the isolated Mo(CO)4[P(OPh)3]2 complex is the cis isomer.
Group theory is widely used in organic and inorganic chemistry. Let's look at a few examples.
Raman spectroscopy detects molecular vibrations that involve changes in polarizability in the electron cloud. A symmetrical stretch in CO2 does not change the dipole moment, and therefore is not IR-active. However, electrons moving away from nuclei change the polarizability, making the stretch Raman-active. Group theory can identify Raman-active vibrational modes by following the same general method used to identify IR-active modes.
Molecular orbital theory, or MO theory, is a model used to describe bonding in molecules. Adding and subtracting the atomic orbitals of two atoms leads to the formation of molecular orbital diagrams of simple diatomics.
To generate MO diagrams of transition metal complexes, scientists use group theory to generate symmetry-adapted linear combinations of atomic orbitals to represent the outer atoms or ligands. This is achieved by generating reducible representations of the ligand atomic orbitals, and then reducing this to an irreducible representation.
The symmetry representations of the metal center and the symmetry-adapted linear combinations are compared in the diagram. In this model, orbitals with the same symmetry overlap to form two molecular orbitals.
You've just watched JoVE's introduction to group theory. You should now be familiar with the underlying principles of molecular symmetry, finding the point group of a molecule, and some examples of how group theory is used in organic and inorganic chemistry. Thanks for watching!
Subscription Required. Please recommend JoVE to your librarian.
Results

Figure 5. IR of Mo(CO)4[P(OPh)3]2.
Solution IR in saturated hydrocarbon (cm-1): 2046 (s), 1958 (s), 1942 (vs).
The fourth resonance can only be seen under high-resolution conditions. Therefore, it is possible, as in this case, that only 3 of the 4 resonances are observed.
Based on the obtained IR, we can conclude that cis-isomer of Mo(CO)4[P(OPh)3]2 was isolated.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
In this video, we learned how to use group theory to predict the number of IR active vibrational modes in a molecule. We synthesized the molecule Mo(CO)4[P(OPh)3]2 and used IR to determine which isomer was isolated. We observed that the product had three C-O vibrations in its IR spectrum, which is consistent with the cis-isomer.
Group theory is a powerful tool that is used by chemists to not only predict IR active vibrational modes, but also vibrational, rotational, and other low-frequency modes observed in Raman spectroscopy. Additionally, group theory is implemented in molecular orbital (MO) theory, which is the most widely used model to describe bonding within transition metal complexes. MO diagrams, used by organic and inorganic chemists, can predict and explain a molecule's observed reactivity.
1st, 2nd, and 3rd row metal carbonyl complexes are used widely in inorganic synthesis as metal precursors for more complex organometallic compounds. Some of the most common types of reactions with metal carbonyl complexes include CO ligand substitution, redox at the metal center, and nucleophilic attack at the CO unit. Metal carbonyl complexes themselves are widely used in catalysis. For example, hydroformylation, the industrial production of aldehydes from alkenes, is catalyzed by the metal carbonyl complex HCo(CO)3 (Figure 6).

Figure 6. Hydroformylation by the metal carbonyl complex HCo(CO)3.
Subscription Required. Please recommend JoVE to your librarian.
References
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).




