Overview
Source : Tamara M. Powers, département de chimie, Texas A & M University
Des complexes de métaux carbonyles sont utilisés comme précurseurs métalliques pour la synthèse de complexes organométalliques comme catalyseurs. La spectroscopie infrarouge (IR) est l’une des méthodes plus utilisées et informative caractérisation de CO contenant des composés. Théorie des groupes, ou l’utilisation des mathématiques pour décrire la symétrie d’une molécule, fournit une méthode pour prédire le nombre d’IR actif C-O modes vibratoires au sein d’une molécule. Observer expérimentalement que le nombre de C-O s’étend dans l’IR est une méthode directe pour établir la géométrie et la structure du métal carbonyle complex.
Dans cette vidéo, nous résumera le molybdène carbonyle complexe Mo(CO)4P(OPh)3]2, qui peuvent exister dans les formes cis et trans -(Figure 1). Nous allons utiliser la théorie des groupes et spectroscopie IR pour déterminer quel isomère est isolé.
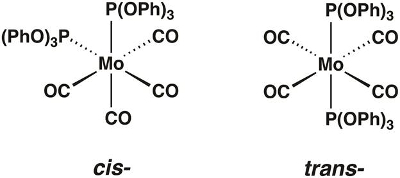
Figure 1. Le cis- et trans-isomères du Mo(CO)4P(OPh)3]2.
Principles
Règles de sélection :
Règles de sélection déterminent le nombre de transitions électroniques, d’un état quantique à l’autre, qu’il est possible pour une molécule donnée. Spectroscopie infrarouge sondes les transitions vibrationnelles du niveau fondamental de la molécule, v = 0, et le premier état excité, v = 1. Le nombre de degrés de liberté de vibration (modes normaux de vibration) pour les molécules linéaires et non linéaires peut être calculé à l’aide de l’équation 1 et 2 de l’équation, respectivement.
3N - 5 (1)
3N - 6 (2)
où N = le nombre d’atomes dans la molécule
Pour un mode normal de vibration pour être IR actif, dipolaire de la molécule doit changer. Par conséquent, les modes normaux de vibration où un changement de dipôle ne se produit pas sont IR inactif. Le nombre des modes actifs de IR peut être déterminé à l’aide de la théorie des groupes.
Théorie des groupes:
Chimistes utilisent la théorie des groupes pour comprendre la relation entre la symétrie et propriétés physiques d’une molécule. Alors que le champ d’application de la théorie des groupes est trop large pour couvrir avec rigueur dans cette vidéo, nous allons fournir les outils nécessaires pour appliquer la théorie des groupes pour des complexes de coordination simples et montrer comment il peut être utilisé pour prédire le nombre de modes de vibration actives IR. Pour illustrer, nous marcherons à travers l’application de la théorie des groupes à la molécule cis -Mo(CO)4[P(OPh)3]2.
Tout d’abord, nous devons déterminer le groupe ponctuel de la molécule. Groupes ponctuels sont utilisés pour décrire les éléments de symétrie présents dans une molécule donnée. Pour déterminer le groupe ponctuel de cis -Mo(CO)4P(OPh)3]2, nous pouvons utiliser un diagramme appelé un arbre de la symétrie, qui pose une série de questions sur les éléments de symétrie présents dans la molécule (Figure 2). Le tableau 1 récapitule tous les éléments de symétrie dans l’arbre de la symétrie. À l’aide de l’arborescence de la symétrie et en supposant que les ligands P(OPh)3 sont point des ligands (tout en ignorant la symétrie de ces ligands), nous trouvons que cis -Mo(CO)4P(OPh)3]2 est dans le groupe point C 2v.

Figure 2. Arbre de symétrie utilisé pour la détermination du groupe point.
Table 1. Éléments de symétrie utilisé au point détermination du groupe.
| Élément de symétrie | Symbole utilisé | Exemple * |
| Identité | E |  |
| Axe de rotation (rotation de 360 ° /n) |
C n |  |
| Plan de symétrie horizontale (réflexion sur le plan xy) |
Σ h |  |
| Plan de symétrie vertical (réflexion sur le plan xz ou yz) |
Σ v |  |
| Plan de symétrie diagonale (réflexion entre les plans xz et yz) |
Σ d |  |
| Centre d’inversion | J’ai |  |
| Axe de rotation impropre (rotation de 360 ° /n suivie de réflexion perpendiculaire à l’axe de rotation) |
S n |  |
| * Exemples correspondent à un complexe octaédrique, où les ligands 1–6 sont équivalentes. Lors de l’opération, la molécule qui en résulte doit être distinguée de sa configuration d’origine. | ||
Pour la prochaine étape, nous devons introduire les tables de caractères, qui décrivent tous la symétrie présente au sein d’un groupe de point donné. La table de caractères pour le point groupe C2v est illustrée ci-dessous.
| C 2v | E | C 2 | Σ v (xz) | Σ v ' (yz) | ||
| A 1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A 2 | 1 | 1 | −1 | −1 | Rz | XY |
| B 1 | 1 | −1 | 1 | −1 | x, R,y | XZ |
| B 2 | 1 | −1 | −1 | 1 | y, R,x | YZ |
Le groupe point est indiqué dans le coin supérieur gauche de la table de caractères. À droite du groupe point, toutes les opérations de symétrie inhérentes à ce groupe de point sont répertoriés.Les lignes suivantes listent toutes les représentations de symétrie (représentations irréductibles, représentées par des symboles de Mulliken, personne1) figurant dans ce groupe de point, ainsi que de la symétrie des fonctions qui peuvent nous parler de la symétrie de orbitales atomiques ainsi que des mouvements linéaires le long des x, y et z.
À l’aide de la table de caractères pour le point groupe C2v, nous générons une représentation réductible (Γrouge) des modes d’élongation C-O dans la molécule cis -Mo(CO)-4[P(OPh)3]2 (Figure 3 ). La représentation réductible, ou la combinaison linéaire de représentations irréductibles, peuvent être générée en appliquant chacune des opérations de symétrie au sein de la table de caractères pour les vibrations au sein de la molécule et en enregistrant le nombre de vibrations de C-O qui restent inchangés (dans la même position dans l’espace). Par exemple, dès la mise en l’élément de symétrie d’identité aux vibrations C-O en cis -Mo(CO)4P(OPh)3]2, tous les quatre des flèches vibrationnelles restent dans la même position. Par conséquent, la première valeur dans notre représentation réductible est 4. Si nous continuons à cet exercice, nous allons générer la représentation réductible ci-dessous.
| C 2v | E | C 2 | Σ v (xz) | Σ v ' (yz) |
| Γ rouge | 4 | 0 | 2 | 2 |
Ensuite, nous utilisons la table de caractères C2v pour trouver la combinaison linéaire des représentations irréductibles qui génère Γrouge pour les vibrations de C-O dans les cis -Mo(CO)4[P(OPh)3]2. Réduction de la représentation réductible peut être obtenue à l’aide de la formule de réduction indiquée dans l’équation 3.
 (3)
(3)
où :
nj’ai = nombre de fois où la représentation irréductible j’ai se produit dans la représentation réductible
h = ordre du groupe (nombre total d’opérations de symétrie)
c = la classe de fonctionnement
gc = nombre d’opérations dans la classe
Χ j’ai = caractère de la représentation irréductible pour les opérations de la classe
Χ r = caractère de la représentation réductible pour les opérations de la classe
En utilisant l’équation 3 pour chacune des représentations irréductibles dans la table de caractères C,2v, nous trouvons que Γrouge = 2A1 , B1 + B2. Les trois les représentations irréductibles qui contribue A1, B1et B2, sont IR actif, parce qu’ils se transforment comme le x-, y-ou axe z (voir la symétrie des fonctions dans le table des caractères). Par conséquent, nous prédisons que cis -Mo(CO)4P(OPh)3]2 exposera les 4 modes de vibration de C-O dans son spectre IR.
Pour résumer, les étapes suivantes sont nécessaires afin de déterminer le nombre de modes de vibration actives IR dans une molécule :
1. Déterminez le groupe ponctuel de la molécule.
2. générer une représentation réductible des vibrations d’élongation C-O dans la molécule.
3. réduire la représentation réductible à l’aide de l’équation 3.
4. déterminer le nombre de représentations irréductibles translationnelles présents dans la représentation réduite de l’étape 3.
Si nous suivons ces 4 étapes avec trans -Mo(CO)4P(OPh)3]2, on constate que la molécule possède seulement 1 mode de vibration actif C-O.

Figure 3. CO vibrationnelle s’étend au cis-Mo(CO)4P(OPh)3]2.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. le programme d’installation de la ligne de Schlenk (pour une procédure plus détaillée, veuillez consulter la vidéo de « Schlenk lignes transfert de solvant » dans la série Essentials of Organic Chemistry ). Sécurité de canalisation de Schlenk devrait être révisée avant la tenue de cette expérience. Verrerie doit être inspecté pour fissures étoiles avant utilisation. Il faut pour s’assurer que O2 n’est pas condensée dans le piège de ligne Schlenk si vous utilisez le liquide N2. À température2 N, O2 se condense et est explosif en présence de solvants organiques. Si l'on soupçonne que O2 a été condensée ou un liquide bleu est observé dans le piège froid, laissez le piège froid sous vide dynamique. Ne pas enlever le liquide N2 collecteur ou éteignez la pompe à vide. Au fil du temps le liquide O2 sera sublime dans la pompe ; Il est sécuritaire d’enlever le piège de2 N liquid une fois tous les O2 a sublimé.
- Fermez le robinet de purge.
- Allumez le gaz2 N et la pompe à vide.
- Comme le Schlenk ligne vide atteint sa pression minimale, préparer le piège froid avec liquide N2 ou neige carbonique et d’acétone.
- Assembler le piège froid.
2. synthèse de Mo(CO)4P(OPh)3]2 (Figure 4)1
Remarque : Utiliser des techniques de ligne Schlenk standard pour la synthèse de Mo(CO)4P(OPh)3]2 (voir la vidéo de « Synthèse d’une ligne de TI métallocène Using Schlenk Technique »). Des complexes de métaux carbonyles sont une source de CO libre, qui est très toxique. Intoxication au monoxyde de carbone se produit lorsque le CO se lie à l’hémoglobine, ce qui entraîne une réduction significative de l’apport d’oxygène à l’organisme. Par conséquent, il est extrêmement important de prendre des mesures de sécurité appropriées lorsque la gestion et l’utilisation avec des complexes de métaux carbonyles. Réactions qui génèrent des CO libre doivent être réalisée sous une hotte ventilée pour prévenir l’exposition à des gaz toxique.
- Ajouter 1,6 g (4,92 mmol) Mo(CO)4(nbd) (nbd = 2, 5-norbornadiène) et le phosphite de triphényle 1,6 mL (9,84 mmol) (P(OPh)3) dans un ballon de Schlenk 100 mL et préparer le ballon de Schlenk le transfert de la canule de solvant.
Remarque : Mo(CO)4(nbd) ((Bicyclo[2.2.1]hepta-2,5-diene)tetracarbonylmolybdenum(0)) peut être acheté chez Sigma Aldrich ou synthétisés à l’aide de méthodes de littérature. 2 - Ajouter 20 mL de dichlorométhane dégazée dans le ballon de Schlenk via transfert de canule.
- Remuer le mélange réactionnel pendant 4 h à température ambiante sous N2.
- Supprimer les substances volatiles sous vide et le lavage de l’entraînant précipitent avec hexanes froids (deux lavages chacune 10 ml, −78 ° C).
- Sécher le produit solid sous vide pendant 15 min.
- Mesurer le spectre IR du produit dans une solution de hexanes.

La figure 4. Synthèse de Mo(CO)4P(OPh)3]2.
Théorie des groupes est un modèle mathématique reliant la symétrie moléculaire aux propriétés telles que des modes de vibration IR-active.
Chaque molécule peut être classé avec un point de groupe, qui décrit chaque élément de symétrie présents dans une molécule par rapport à un point fixe.
Théorie des groupes fournit des tables spéciales, appelées tables de caractères, pour prévoir l’effet de symétrie de la molécule sur ses modes de vibration et d’autres propriétés importantes.
Cette vidéo va discuter les principes qui sous-tendent la théorie des groupes, illustrent la procédure pour la synthèse et la caractérisation d’un isomère de la Mo(CO)4P(OPh)3]2et introduire quelques applications de la théorie des groupes en chimie.
Symétrie moléculaire décrit les configurations impossibles à distinguer d’une molécule. Les transformations entre eux sont appellent des opérations de symétrie, qui surviennent en ce qui concerne un ou plusieurs éléments de symétrie.
Les cinq éléments de symétrie sont les axes de rotation correcte et incorrecte, les avions de miroir, centres d’inversion et identité. Chaque molécule est l’élément neutre , ou E, dans lequel aucun changement se produit.
Un plan de symétrie, étiqueté σ, est un avion de réflexion avec le début et la fin des configurations identiques. Molécules peuvent avoir plus d’un plan de symétrie. Un Centre d’inversion, étiqueté j’ai, est un point par lequel chaque atome est reflété.
Un axe de rotation approprié est un axe autour duquel une molécule tourne à une configuration identique. Il est labellisé Cn, où n est divisé par l’angle de rotation de 360.
Un axe de rotation impropre , étiqueté Sn, est l’axe autour de laquelle une molécule est tournée, puis traduit par un plan de symétrie perpendiculaire. Molécules peuvent avoir plus d’un axe de rotation. L’axe avec le plus haut n est le principal axe.
Molécules sont assignés au point des groupes à l’aide d’un arbre de la symétrie, qui identifie les opérations de symétrie nécessaires pour classer la molécule.
Par exemple, BF3 est non linéaire. Il le fait pas avec au moins deux axes avec n supérieur à 2. Il a au moins un axe de rotation ; son axe principal est C3. Il a trois C2 axes perpendiculaires à l’axe principal et un plan de symétrie perpendiculaire à son axe principal. Ainsi, le trifluorure de bore appartient au groupe point D3 h .
Chaque groupe de point a une table de caractères énumérant ses opérations de symétrie essentiel. Chaque ligne contient une représentation irréductible des opérations, ainsi que les orbitales atomiques correspondants et les mouvements linéaires.
Les représentations réductibles sont générées en évaluant l’incidence de ces opérations de symétrie propriétés moléculaires. Réduire cette représentation donne les représentations irréductibles contributifs.
Maintenant que vous comprenez les principes de la théorie des groupes, Let ' s go grâce à une procédure pour la synthèse d’un isomère de Mo(CO)4P(OPh)3]2 et en comparant son spectre IR au nombre de modes de IR-active prévue pour chaque isomère de théorie des groupes.
Pour commencer la procédure, fermer le conduit d’évacuation de la ligne Schlenk et démarrer le flux de gaz2 N.
Sous une hotte, mesurer 0,5 g de Mo(CO)4(nbd) et placer le précurseur de molybdène dans un ballon jaugé de 200 mL Schlenk. Équiper le ballon à réaction avec une barre de mélanger et boucher le ballon avec un bouchon en verre. Raccorder le ballon à la ligne de Schlenk via le bras latéral, et préparer le ballon pour le transfert de la canule par évacuer le navire pendant 5 minutes, suivie de remplir à nouveau le ballon avec N2. Répétez cette évacuation, puis remplir le processus 3 fois au total.
Ensuite, préparer un autre ballon de Schlenk muni d’un septum en caoutchouc contenant 20 mL de CH2Cl2. Raccorder le ballon à la ligne de Schlenk et sécuriser la fiole dans la hotte. À l’aide d’une seringue, dresser mL 0,87 de phosphite de triphényle et dispensent dans le ballon de Schlenk. Assurez-vous que le robinet d’arrêt ligne Schlenk est ouvert au N2. Dégazer le CH2Cl2/triphenyl mélange du phosphite de bouillonnement N2 par le solvant pendant 10 minutes. Puis utilisez transfert de canule pour ajouter la solution dans le ballon contenant le solide. Ouvrez le ballon à réaction au gaz2 N et remuez le mélange à température ambiante pendant 4 heures.
Une fois la réaction terminée, remplacer le bouchon de caoutchouc avec un bouchon en verre et éliminer les solvants volatils sous vide.
Ajouter hexanes au produit qui en résulte et refroidir dans un bain de glace carbonique/acétone brièvement, jusqu'à ce qu’un précipité formes. Filtrer le précipité et laver le précipité deux fois avec 10 mL de froids hexanes et recueillir le solide par filtration. Sécher le produit solide sous vide pendant 15 minutes.
Enfin, dissoudre une partie du produit en hexanes et chargez la solution dans une cellule IR. Acquérir un spectre IR du complexe.
Maintenant, nous allons déterminer si le produit est le cis ou isomère trans en assignant des groupes pointez les deux isomères et comparant les modes d’IR-active prévues pour le spectre IR.
Ni la CEI ni trans isomère est linéaire, et n’a plus de deux axes de rotation avec l’ordre supérieur à 2. Les deux ont au moins un axe de rotation. Les axes principaux pour les isomères cis et trans sont C2 et C4, respectivement.
L’isomère cis n’a pas deux C2 axes perpendiculaires à l’axe de2 C, n’a-t-elle un plan de symétrie perpendiculaire. Il dispose de deux avions de miroir contenant l’axe de2 C, donc son groupe ponctuel est C,2v. L’isomère trans a quatre C2 axes et un plan de symétrie perpendiculaire à son axe de4 C, donc son groupe ponctuel est D4 h.
Ensuite, diluable représentations des tronçons CO sont générées en appliquant chaque opération de symétrie de la molécule et compter les tronçons de C-O qui ne changent pas d’emplacement dans l’espace.
La table de2v Ccomporte quatre opérations : identité, rotation2 Cet réflexions par le biais de deux miroirs plans contenant l’axe de2 C. Dans l’opération identité, tous les moments dipolaires quatre restent en place. Tous les quatre moments dipolaires prendre différentes positions après une rotation de2 C. Deux moments dipolaires restent dans la même position pour chaque réflexion.
La formule de réduction calcule le coefficient de chaque représentation irréductible dans la représentation réductible. La motion groupe ordre est le nombre d’opérations de symétrie. Les classes sont des types d’opérations de symétrie. Ici, le nombre d’opérations dans chaque classe est 1, qui est traditionnellement exclus d’un tableau de caractères.
Le caractère est la valeur correspondant à une représentation pour une classe donnée. Lorsque la formule de réduction est appliquée, trois représentations irréductibles sont retrouvent, avec un se produisant deux fois. Ces représentations se transforment comme axe soit le x, you z , ce qui correspond à quatre tronçons de IR-active C-O.
En utilisant la même technique, l’isomère trans s’avère pour présenter un tronçon de IR-active C-O. Le spectre IR du produit molybdène a pics à 2046, 1958 et 1942 cm-1. Avec des données de résolution plus élevées, on peut observer une quatrième portion C-O. Basé sur l’IR obtenue, on peut conclure que l’isolé Mo(CO)4P(OPh)3]2 complexe est l’isomère cis .
Théorie des groupes est largement utilisée en chimie organique et inorganique. Regardons quelques exemples.
La spectroscopie Raman détecte les vibrations moléculaires qui impliquent des changements dans la polarisabilité dans le nuage d’électrons. Un étirement symétrique en CO2 ne change pas de moment dipolaire et donc n’est pas activé par IR. Toutefois, les électrons s’éloigne des noyaux changent la polarisabilité, rendant l’étirement actif Raman. Théorie des groupes peut identifier des modes de vibration Raman-active en suivant la même méthode générale permet d’identifier les modes de IR-active.
Théorie des orbitales moléculaires, ou théorie de l’OM, est un modèle utilisé pour décrire les liaisons dans les molécules. Additionner et soustraire les orbitales atomiques des deux atomes conduisent à la formation de molecular orbitales diagrammes de simple diatomiques.
Pour générer des diagrammes de MO des complexes de métaux de transition, les scientifiques utilisent la théorie des groupes pour générer adaptées à la symétrie des combinaisons linéaires d’orbitales atomiques pour représenter les atomes externes ou des ligands. Ceci est réalisé en générant des représentations réductibles des orbitales atomiques ligand et puis réduire cela à une représentation irréductible.
Les représentations de la symétrie du centre métallique et les combinaisons linéaires adaptées à la symétrie sont comparées dans le diagramme. Dans ce modèle, les orbitales avec la même symétrie se chevauchent pour former deux orbitales moléculaires.
Vous avez juste regardé introduction de Jupiter à la théorie des groupes. Vous devriez maintenant être familiarisé avec les principes de symétrie moléculaire, trouver le groupe ponctuel d’une molécule et quelques exemples d’utilisation de la théorie des groupes en chimie organique et inorganique. Merci de regarder !
Subscription Required. Please recommend JoVE to your librarian.
Results

Figure 5. IR de Mo(CO)4P(OPh)3]2.
Solution IR en hydrocarbure saturé (cm-1) : 2046 (s), 1958 (s), 1942 (vs).
La quatrième résonance n’est visible que dans des conditions de haute résolution. Par conséquent, il est possible, comme en l’espèce, que seulement 3 des 4 résonances sont observées.
Basé sur l’IR obtenu, nous pouvons conclure cet isomère cis Mo(CO)4[P(OPh)3]2 a été isolé.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
Dans cette vidéo, nous avons appris comment utiliser la théorie des groupes pour prédire le nombre de modes de vibration actives IR dans une molécule. Nous avons synthétisé la molécule Mo(CO)4P(OPh)3]2 et IR permettant de déterminer quel isomère a été isolé. Nous avons observé que le produit avait trois vibrations C-O dans son spectre IR, ce qui est conforme à la CEI-isomère.
Théorie des groupes est un outil puissant qui est utilisé par les chimistes de prévoir non seulement actives modes vibrationnels d’IR, mais aussi vibration, rotation et les autres modes de basse fréquence observées dans la spectroscopie Raman. En outre, la théorie des groupes est implémentée dans (MO) théorie des orbitales moléculaires, qui est le modèle le plus utilisé pour décrire les liaisons au sein des complexes de métaux de transition. Les diagrammes de MO, utilisées par les chimistes organiques et inorganiques, peuvent prédire et expliquer la réactivité observées d’une molécule.
1st, 2èmeet 3rd row carbonyles métalliques complexes sont largement utilisés en synthèse inorganique comme précurseurs métalliques pour les composés organométalliques plus complexes. Certains des types plus communs de réactions avec des complexes de métaux carbonyles comprennent CO ligand substitution, oxydo-réduction au centre métallique et une attaque nucléophile de l’unité de CO. Les complexes métal carbonyle se sont largement utilisés dans la catalyse. Par exemple, hydroformylation, la production industrielle des aldéhydes à partir d’alcènes, est catalysée par les carbonyles métalliques complexes HCo(CO)3 (Figure 6).

Figure 6. Hydroformylation par le métal carbonyle complexe HCo(CO)3.
Subscription Required. Please recommend JoVE to your librarian.
References
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).




