- 00:08Overview
- 01:08Principles of X-ray Diffraction
- 04:43Instrument, Sample and Beam Parameters
- 05:57Selection of the Parameters for the Acquisition
- 06:24Acquisition and Analysis
- 07:04Results
- 07:48Applications
- 08:58Summary
Röntgenbeugung
English
Share
Overview
Quelle: Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA
Röntgenbeugung (XRD) ist eine Technik, die in der Materialwissenschaft zur Bestimmung der atomaren und molekularen Struktur eines Materials verwendet wird. Dies geschieht, indem eine Probe des Materials mit einfallenden Röntgenstrahlen bestrahlt und dann die Intensitäten und Streuwinkel der Röntgenstrahlen gemessen werden, die vom Material gestreut werden. Die Intensität der gestreuten Röntgenstrahlen wird in Abhängigkeit vom Streuwinkel dargestellt, und die Struktur des Materials wird aus der Analyse der Position, des Winkels und der Intensitäten der streunenden Intensitätsspitzen bestimmt. Neben der Möglichkeit, die durchschnittlichen Positionen der Atome im Kristall zu messen, können Informationen darüber bestimmt werden, wie die tatsächliche Struktur von der idealen abweicht, die sich beispielsweise aus interner Belastung oder aus Defekten ergibt.
Die Beugung der Röntgenstrahlen, die für die XRD-Methode von zentraler Bedeutung ist, ist eine Teilmenge der allgemeinen Röntgenstreuphänomene. XRD, das im Allgemeinen verwendet wird, um zu bedeuten, kann Weitwinkel-Röntgenbeugung (WAXD) können, fällt unter mehrere Methoden, die die elastisch gestreuten Röntgenwellen verwenden. Andere elastische Streutechniken auf Röntgenbasis umfassen die Röntgenstreuung mit kleinen Winkeln (SAXS), bei der die Röntgenstrahlen auf der Probe über den kleinen Winkelbereich von 0,1-100 in der Regel einfallen. SAXS misst strukturelle Korrelationen der Skala von mehreren Nanometern oder größer (z. B. Kristallaufbauten) und Röntgenreflektivität, die die Dicke, Rauheit und Dichte von Dünnschichten misst. WAXD deckt einen Winkelbereich über 100ab.
Principles
Beziehung zwischen diffracted Spitzenpositionen und Kristallstruktur:
Wenn Lichtwellen von ausreichend kleiner Wellenlänge auf ein Kristallgitter einfallen, diffraktieren sie von den Gitterpunkten. Bei bestimmten Einfallswinkeln stören die diffrierten parallelen Wellen konstruktiv und erzeugen nachweisbare Intensitätsspitzen. W.H. Bragg identifizierte die in Abbildung 1 dargestellte Beziehung und leitete eine entsprechende Gleichung ab:
n n = 2dhkl sin
Hier bei der Wellenlänge der verwendeten Röntgenstrahlen ist dhkl der Abstand zwischen einem bestimmten Satz von Ebenen mit (hkl) Miller-Indizes*, und – ist der Einfallswinkel, bei dem ein Beugungsgipfel gemessen wird. Schließlich ist n eine ganze Zahl, die die “harmonische Ordnung” der Beugung darstellt. Bei n=1 haben wir z.B. die erste Oberschwingung, was bedeutet, dass der Pfad der Röntgenstrahlen, der durch den Kristall diffracted wird (entspricht 2dhkl sin ) genau 1,während bei n=2 der diffrierte Pfad 2‘ist. Typischerweise können wir n=1 und im Allgemeinen n=1 für sin-1(2’/dh’k’l’) annehmen, wobei h’k’l’ die Miller-Indizes der Ebenen sind, die den ersten Peak (bei dem niedrigsten 2-Wert) in einem Beugungsexperiment anzeigen. Miller-Indizes sind eine Gruppe von drei ganzzahlwenigen, die ein Notationssystem zum Identifizieren von Richtungen und Ebenen innerhalb von Kristallen bilden. Für Richtungen stellen die [h k l] Miller-Indizes die normalisierte Differenz in den jeweiligen x-, y- und z-Koordinaten (in einem kartesischen Koordinatensystem) von zwei Punkten entlang der Richtung dar. Bei Ebenen sind die Miller-Indizes (h k l) einer Ebene einfach die h k l Werte der Richtung senkrecht zur Ebene.
In einem typischen XRD-Experiment im Reflexionsmodus wird die Röntgenquelle in Position gebracht und die Probe in Bezug auf den Röntgenstrahl über . Ein Detektor nimmt den diffrierten Strahl auf und muss mit der Probenrotation Schritt halten, indem er mit der doppelten Geschwindigkeit rotiert (d. h. für einen gegebenen Probenwinkel von – ist der Detektorwinkel 2 “). Die Geometrie des Experiments ist schematisch in Abbildung 1 dargestellt.
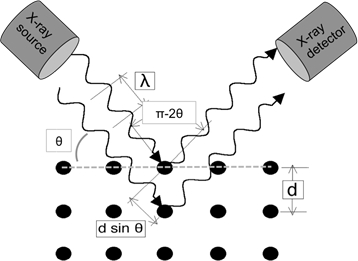
Abbildung 1: Illustration von Braggs Gesetz.
Wenn ein Spitzenwert in der Intensität beobachtet wird, ist Gleichung 1 notwendigerweise erfüllt. Folglich können wir d-Abstände basierend auf den Winkeln berechnen, in denen diese Spitzen beobachtet werden. Durch die Berechnung der d-Spacings mehrerer Peaks können die Kristallklasse und die Kristallstrukturparameter material sample mithilfe einer Datenbank wie dem Hanawalt Search Manual oder Datenbankbibliotheken identifiziert werden, die mit der verwendeten XRD-Software verfügbar sind.
Wir gehen davon aus, dass es sich bei der untersuchten Probe nicht um einen einzigen Kristall handelt. Wäre die Probe ein einzelner Kristall mit einer bestimmten (h*k*l*) Ebene parallel zur Probenoberfläche, müsste sie gedreht werden, bis die Bragg-Bedingung für die (h*k*l*) erfüllt ist, um eine Spitze in diffracted Intensität (für n=1) mit potenziell höheren harmonischen (h*k*l*) Spitzen (z.B. für n=2) auch in höheren Winkeln nachweisbar zu sehen. Bei allen anderen Winkeln gäbe es keine Spitzen in einer einzigen Kristallprobe. Nehmen wir stattdessen an, dass die Probe entweder polykristallin ist oder dass es sich um ein Pulver handelt, mit einer statistisch signifikanten Anzahl von kristallinen Körnern oder Pulverpartikeln, die durch den einfallenden Röntgenstrahl beleuchtet werden. Unter dieser Annahme besteht die Stichprobe aus zufällig orientierten Körnern, mit einer ähnlichen statistischen Wahrscheinlichkeit für alle möglichen Gitterebenen zu diffract.
Die Beziehungen zwischen dem dhkl und den Einheitenzellparametern sind unten in den Gleichungen 2-7 für die 7 Kristallklassen, kubisch, tetragonal, sechseckförmig, rhombohedral, orthorhombic, monoclinic und triclinic dargestellt. Die Einheitenzellenparameter bestehen ausLängen von(a,b,c) und den Winkeln zwischen den Kanten der Einheitszellen für die 7 Kristallklassen (Abbildung 1x zeigt das Beispiel einer der Kristallklassen: die tetragonale Struktur, wobei a=bc und s = = 900). Mit mehreren diffragierten Spitzenpositionen (d.h. mehreren unterschiedlichen dhkl-Werten) können die Werte der Einheitenzellparameter eindeutig gelöst werden.
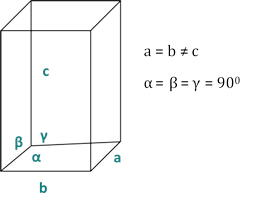
Abbildung 2: Die tetragonale Struktur als eine der sieben Kristallklassen.
Kubisch (a = b = c; n = n = 900):
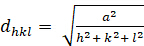 [2]
[2]
Tetragonal (a = b – c; – = n = 900):
 [3]
[3]
Hexagonal (a = b – c; – = 900; n = 1200):
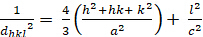 [4]
[4]
Orthorhombic (a b – c; – = n = 900):
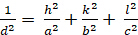 [5]
[5]
Rhombohedral (a = b – c; – = n = 900):
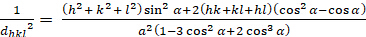 [6]
[6]
Monoklin (a b – c; – = 900€ )
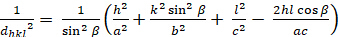 [7]
[7]
Triklinisch (a b – c; – , 900)
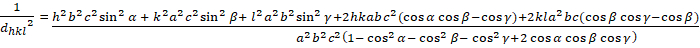 [8]
[8]
Beziehung zwischen diffracted Spitzenintensitäten und Kristallstruktur:
Als nächstes untersuchen wir die Faktoren, die zur Intensität in einem XRD-Muster beitragen. Die Faktoren können als 1) den Beitrag zur Streuung aufschlüsseln, der sich direkt aus den einzigartigen strukturellen Aspekten des Materials ergibt (die spezifischen Typen und Positionen von Streuatomen in der Struktur) und 2) denen, die nicht spezifisch für das Material sind. Im ersten Fall gibt es zwei Faktoren: den “Absorptionsfaktor” und den “Strukturfaktor”. Der Absorptionsfaktor hängt in erster Linie von der Fähigkeit des Materials ab, Röntgenstrahlen auf ihrem Weg ein- und ausgehen zu absorbieren. Dieser Faktor hat keine Abhängigkeit, solange die Proben nicht dünn sind (die Probe sollte > 3-mal dicker sein als die Dämpfungslänge der Röntgenstrahlen). Mit anderen Worten, der Beitrag des Absorptionsfaktors zur Intensität verschiedener Spitzen ist konstant. Der “Strukturfaktor” wirkt sich direkt auf die Intensität bestimmter Spitzen als direkte Folge der Struktur aus. Die übrigen Faktoren, die “Multiplizität”, die alle Ebenen, die zur gleichen Familie gehören, weil sie symmetrisch verwandt sind, und der Faktor “Lorentz-Polarisierung”, der aus der Geometrie des XRD-Experiments stammt, wirken sich auch auf die relative Intensität der Spitzen, aber sie sind nicht spezifisch für ein Material und können leicht mit analytischen Ausdrücken berücksichtigt werden (d.h. XRD-Analysesoftware kann sie mit analytischen Funktionen entfernen).
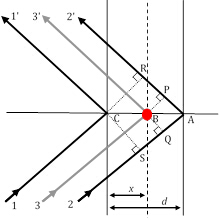
Abbildung 3: Drei Beugungsstrahlpfade, von denen die Strahlen 11′ und 22′ die Bragg-Bedingung erfüllen, während Strahl 33′ aus der Streuung durch ein Atom (roter Kreis) an einer beliebigen Position resultiert.
Als einziger Faktor, der den einzigartigen strukturellen Beitrag eines Materials zu den relativen Intensitäten von XRD-Spitzen trägt, ist der Strukturfaktor sehr wichtig und erfordert einen genaueren Blick. In Abbildung 2 nehmen wir an, dass die Bragg-Beugungsbedingung1. Ordnung (denken Sie daran, dass dies n=1 entspricht) zwischen Strahl11′ und Strahl22′ erfüllt ist, die auf zwei atomaren Ebenen in h00-Richtung (unter Verwendung der zuvor beschriebenen Miller-Indizes-Notation) verstreut sind, die durch einen Abstand d getrennt sind. Unter dieser Bedingung beträgt der Unterschied in der Bahnlänge zwischen Strahl11′ und Strahl22′ (22′-11′) = SA + AR = . Die Phasenverschiebung zwischen den diffrierten Strahlen 1 und 2 ist daher22′-11′ =(22′-11′)/’) 2′ =2′ (unter der Annahme einer kubischen Symmetrie und daher d = a/h in h00-Richtung].
Mit wenigen Schritten in der analytischen Geometrie kann gezeigt werden, dass die Phasenverschiebung,33′-11′), mit strahl 3 diffracted durch eine beliebige Ebene von Atomen, dieeinen beliebigen Abstand xsind, gegeben wird durch: Unter Berücksichtigung der beiden anderen orthogonalen Richtungen (0k0) und (00l) und v=y/a und w=z/a als Bruchkoordinaten in y- und z-Richtung erstreckt sich der Ausdruck für die Phasenverschiebung bis zu . Nun hat die Röntgenwelle, die durch das j-th-Atom in einer Einheitszelle gestreut wird, eine Streuamplitude von fj und eine Phase vonj, so dass die Funktion, die sie 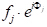 beschreibt, ist. Der Strukturfaktor, den wir suchen, ist daher die Summe aller Streufunktionen aufgrund all der einzigartigen Atome in einer Einheitszelle. Dieser Strukturfaktor F wird wie:
beschreibt, ist. Der Strukturfaktor, den wir suchen, ist daher die Summe aller Streufunktionen aufgrund all der einzigartigen Atome in einer Einheitszelle. Dieser Strukturfaktor F wird wie:
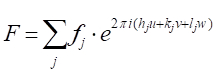 [9]
[9]
und der Intensitätsfaktor, der durch den Strukturfaktor beigesteuert wird, ist I = F2.
Basierend auf den Positionen (u,v,w) von Atomen auf bestimmten Ebenen (h,k,l) besteht die Möglichkeit von Interferenzen zwischen zerstreuten Wellen, die konstruktiv, zerstörerisch oder dazwischen sind, und diese Interferenz wirkt sich direkt auf die Amplitude der XRD-Spitzen aus. die (hkl) Ebenen darstellen.
Nun, ein Diagramm der Intensität, I, im Vergleich zu 2, ist das, was in einem XRD-Experiment gemessen wird. Die Bestimmung des Kristalltyps und der zugehörigen Einheitenzellparameter(a, b, c, , , und )kann analytisch erreicht werden, indem die systematische Anwesenheit/Abwesenheit von Peaks beobachtet wird, wobei die Gleichungen 2-9 verwendet werden, Werte mit Datenbanken verglichen werden, wobei Abzug und ein Prozess der Eliminierung verwendet werden. Heutzutage ist dieser Prozess ziemlich automatisiert durch eine Vielzahl von Software mit Kristallstruktur-Datenbanken verbunden.
Procedure
Results
In Figure 4 we see the XRD peaks for the Ni powder sample. Note that the peaks that are observed (e.g. {111}, {200}) are for those that have either all even or all odd combinations of h, k, and l. Ni is face-centered cubic (FCC), and in all FCC structures, the peaks corresponding to {hkl} planes where h, k, and l are mixtures of even and odd integers, are absent due to the destructive interference of the scattered X-rays. Peaks corresponding to planes, such as {210} and {211} are missing. This phenomenon is called the systematic presence and absence rules, and they provide an analytical tool for assessing the crystal structure of the sample.
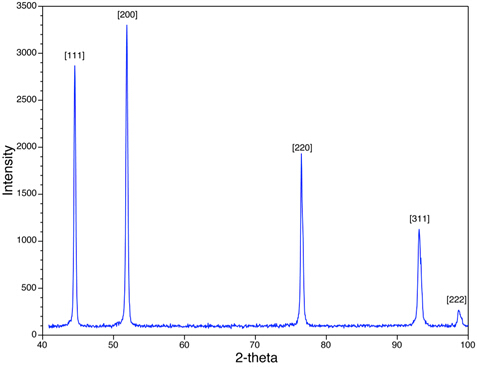
Figure 4: An XRD scan of Ni with a face-centered cubic structure is shown.
Applications and Summary
This is a demonstration of a standard XRD experiment. The material examined in this experiment was in a powder form, but XRD works equally well with solid piece of material as long as the sample has a flat surface that can be set parallel to the plane of the sample stage.
XRD is a fairly ubiquitous method for determining the presence (or absence) of crystallographic order in materials. Beyond the standard application of determining the crystal structure, XRD is often used to obtain a variety of other structural information such as:
- Whether or not the structure of a material is amorphous (characterized by a broad hump in the diffraction intensity and a lack of discernable crystallographic peaks),
- Whether the sample is a composite material consisting of multiple crystallographic phases and, if so, determine the fraction of each phase,
- Determining whether a material is an amorphous/crystalline composite
- Determining the grain/particle size of the material,
- Determining the degree of texture (preferred orientation of grains) in material.
Transcript
X-Ray diffraction is a technique used to determine the atomic and molecular structure of materials. Solids have a crystalline structure, which corresponds to a microscopic arrangement of atoms that is repeated periodically. By staking planes, a 3-D structure of specific symmetry can be formed.
These structural arrangements result in a specific packing geometry that dictates the physical and chemical properties of the material. Such as magnetization, thermal conductivity, or malleability. Reflecting x-rays off of materials can reveal the inner details of their structure.
This video will illustrate the general principles of x-ray diffraction on a material and how this phenomenon is used in the laboratory to determine the structure and chemical composition of materials.
To begin, let’s have a closer look at a crystal. It is formed of atomic lattices disposed in planes periodically separated by a distance dhkl of a few angstroms. H, k, l are Miller indices, a set of three integers the constitute a notation system for identifying directions and planes within crystals. The smallest repeating structure in a crystal is called the unit cell. Different angles, alpha, beta, gamma, and lengths a, b, c, of a unit cell forming the lattice will give rise to different symmetries. There are seven crystal systems. Cubic, tetragonal, orthorhombic, rhombohedral, monoclinic, triclinic, and hexagonal.
The relationship between the unit cell parameters and the Miller indices can be calculated for each crystal class. Electromagnetic of wavelength lambda can have similar dimensions with the differences between planes within the crystal’s lattice. These correspond to wavelengths in the x-ray spectral range. When x-ray light waves irradiate a crystal at an incident angle theta, they propagate through the crystal and encounter lattice points from which they defract. Bragg’s Law relates these parameters where n is an integer that represents the harmonic order of the diffraction. For a given lambda, only specific angles theta give rise to diffraction. This is the unique signature of a crystalline structure.
In an experiment, the sample is rotated and the detector that collects the scattered x-rays records peaks in intensity when reaching these characteristic angles. One can then extract the lattice spacing DHKL for each angle satisfying the Bragg’s Law. Using multiple diffracted peak positions corresponding to several distinct DHKL values, the parameters of the unit cell can be solved uniquely.
Two main factors contribute to the relative intensity of the peaks. First, there are the non-structural contributions, which include the ability of the material to absorb x-ray light, and the geometry of the XRD experiment. These can be taken into account in the post-processing of the experimental data. Second, and most importantly, the structural contribution of the material is carried to the relative intensities of XRD. Each diffraction peak is in fact the sum of all the scattered amplitudes from multiple ray paths diffracted by all the unique atoms in a unit cell. If scattered lights are in phase, there is constructed interference. While if they are out of phase, there is destructed interference. These interferences directly affect the amplitude of the XRD peaks, representing the HKL planes of the crystal.
We will now see how these principles apply in an actual x-ray diffraction experiment.
Before starting, carefully inspect the XRD instrument and assess its status and safety. XRD users must be trained in basic radiation safety before having access to the instrument. Then proceed with sample preparation. In this experiment, we use a nickel powder sample in the form of a pressed pellet.
It is important that the sample is not thin and it should be at least three times thicker than the attenuation length of the x-rays. Note that the following procedure applies to a specific XRD instrument and its associated software and there may be some variations when other instruments are used.
Load the sample in the sample spinner stage and lock the sample into position, making sure the irradiated side of the sample is parallel to the sample stage. Use a mask to adjust the x-ray beam size of the instrument according to the sample diameter. At the smallest incident angle, the beam must have a footprint smaller than the sample width.
Now it is time to choose the acquisition parameters. First, select the angle range for the XRD scan. Typically, the range goes from 15 to 90 degrees. Then, select the degree step size as well as the integration time at each angle scanned.
Next, proceed to the data acquisition. After the scan, a graph of the intensity as a function of the angle to theta is obtained. From this initial scan, select specific peaks and determine peak positions.
Repeat the acquisition and focus this time on a narrower scan range around specific peaks. Using a smaller step size in angle to obtain higher resolution data. Once the data acquisition is finished, data can be analyzed to identify the structure of the material.
Using the instrument software and database library, each peak of the spectrum is identified and associated to a specific symmetry of crystal arrangement. In this particular case of the nickel powder sample, the spectrum shows a first peak corresponding to a one one one symmetry.
The second peak is associated to a two zero zero symmetry and so on. Then the software determines that this specific combination of symmetries corresponds to a face centered cubic structure and it identifies that the sample is a nickel powder.
X-ray diffraction is a standard method for determining the presence or absence of crystallographic order in materials. It is often used to obtain a variety of other structural information regarding internal stress and defects in a crystal, or multiple crystallographic phases in composite materials. XRD technique is also used in biology to determine the structure and spatial orientation of biological macromolecules such as proteins and nucleic acids.
In particular, this is how the double helix structure of DNA has been discovered, leading to the Nobel Prize in Physiology or Medicine in 1962. The study of the geochemistry of minerals either for mining purposes or even for planetary exploration also makes use of XRD technique. Think of the Rover Curiosity on Mars that has amongst its ten scientific instruments an XRD detector to analyze the composition of the martian soil.
You’ve just watched Jove’s introduction to x-ray diffraction. You should now understand the crystalline structure of a solid and the principles of x-ray diffraction. You should also know how the XRD technique is used in the laboratory to obtain the structure and chemical composition of materials.
Thanks for watching!
