晶体场理论 - 八面体络合物

晶体场理论

为了解释观察到的过渡金属复合物 (如颜色) 的行为，开发了一种模型，其中涉及来自配体的电子与中央金属原子未杂交 d 轨道中的电子之间的静电交互。 这种静电模型是晶体场理论 (CFT)。 它有助于了解，解释和预测配位化合物 of 过渡金属的颜色，磁性行为和某些结构。

CFT 侧重于在非金属配体键上的协调复合物中的中心金属离子上的非粘接电子。 像价键理论一样， CFT 只讲述了部分复杂事件的行为。 CFT 以纯净形式忽略配体和金属离子之间的任何共价键合。 配体和金属均被视为无限小点电荷。

所有电子都是负的，因此从配体中捐赠的电子将排斥中心金属的电子。 考虑八面体中未杂交 d 轨道中电子的行为。 如图 1 所示， Five d 轨道由叶形区域组成，并在空间中排列。 在一个八面体中，沿轴的六条配体配位。

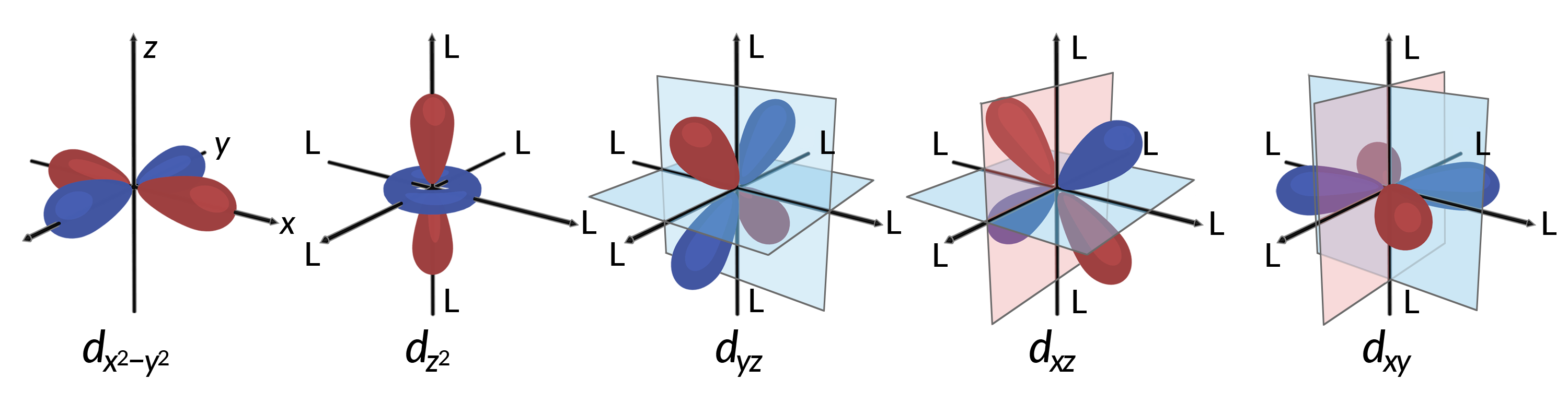
图 1. 此处显示了五 d 轨道的方向特性。 阴影部分表示轨道的相位。 沿八面体络合物轴的配体 (L) 配位。 为了清晰起见， dx2_−Y2 轨道中遗漏了配体，因此可以显示轴标签。

在气相中一个皮肤不全的金属离子中，电子根据 洪德规则（Hund’s rules） 在五个轨道中分布，因为轨道都有相同的能量。 在过渡金属波群中，轨道原子的 d 过渡金属的能量会受到配体类型和分子几何结构的影响。 如果配体分子均匀地分布在金属离子周围，则会产生球形晶体场。 这个球形晶体场通过一个相等的数量来提高金属离子的 d 轨道的能量 (图 2)。 当向八面体几何结构中的金属离子配体配位时， d 轨道的能量就不再相同。

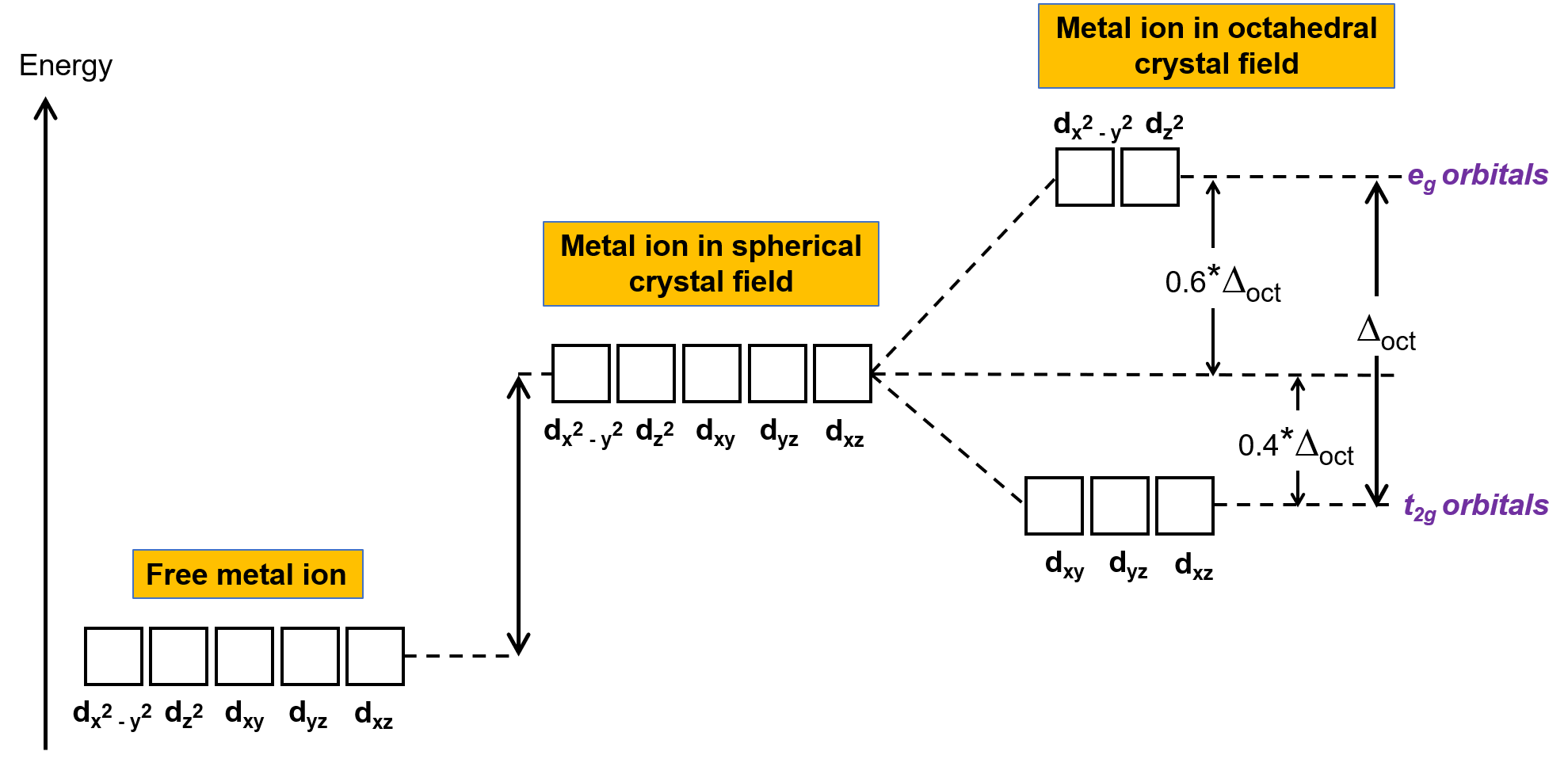
图 2. 球状晶体场中金属离子的 d 轨道与未结肤色的游离金属离子的 d 轨道相比不稳定 (在能量中较高)。 在八面体络合物中，由于配体与直接指向的 d 轨道的交互作用更强，因此 EG 轨道与 t2g 轨道相比更加不稳定 (能量中的值更高)。

在八面体络合物，五个 d 轨道中的两个叶片 dx2_−Y2 和 dz2 轨道指向配体 (图 1)。 这两个轨道称为 EG 轨道 (符号指轨道的对称性)。 另外三个轨道，即 dxy ， dxz 和 dyz 轨道，在配体之间有指向的凸角，称为 t2g 轨道 (该符号也是指轨道的对称性)。 当六条配体沿八面体轴接近金属离子时，它们的点电荷会在金属离子的 d 轨道中重新产生电子。 但是，轨道 (dx2-Y2 轨道) 中的电子与配体之间的脉冲是大于 t2g 轨道 (dxy ， dxz 和 dyz 轨道) 中电子与配体之间的脉冲。 这是因为 EG 轨道的凸缘直接指向配体，而 t2g 轨道的凸缘则指向配体之间。 因此，八面体中金属离子的轨道等电子的潜在能量高于 t2g 轨道中电子的潜在能量。 能量的差异可能如图 2 所示。

EG 和 t2g 轨道之间的能量差异称为晶体分割，由 Δoct 符号表示，其中 oct 代表八面体。  Δoct 的大小取决于许多因素，包括围绕中心金属离子的六条配体的性质，金属上的电荷，以及金属使用的是 3D ， 4D 还是 5d 轨道。 不同的配体产生不同的晶体场碎片。 配体产生的晶体场分裂量不断增加，以光谱化学系列表示，其简短版本如下：

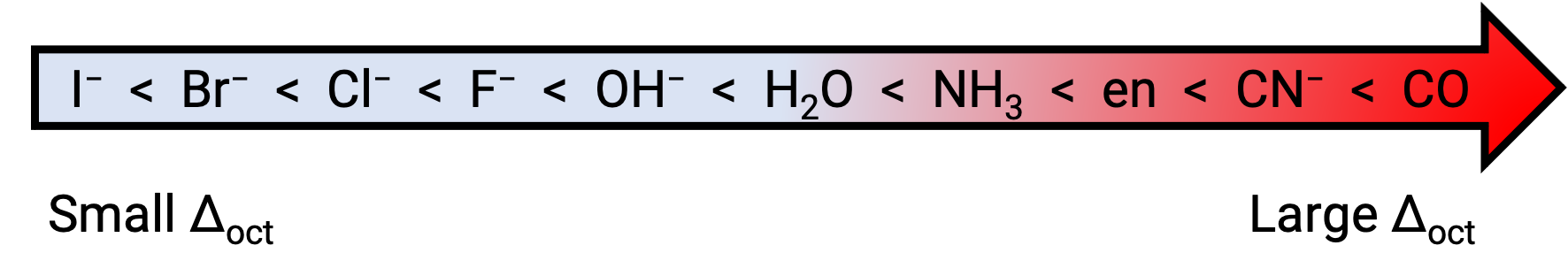
本文改编自 Openstax, 化学 2e, 第19.3节： S 配位化合物的光谱和磁性。