率の法律および反作用の順序を決定します。
English
Share
Overview
ソース: 博士ニール エイブラムスの研究室-環境科学および林業のニューヨーク州立大学
すべての化学反応は、反応しようとして製品の進行状況の定義特定率を持っています。この率は、温度、濃度、反応の物理プロパティによって影響があります。料金は、中間体や遷移状態が形成されるが、反応も製品にも含まれます。率法は反応の各反応の役割を定義し、続行する反応に必要な時間を数学的にモデル化するために使用できます。レート方程式の一般的な形は以下のとおりです。
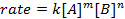
AとBが異なる分子種、 mとnの濃度を反応注文、 kは速度定数。ほぼすべての反応の速度は反応物質が枯渇している、有効な衝突が発生する可能性が低くを作るよう経年変化します。ただし、速度定数は、特定の温度における単一の反作用のため固定されています。反応次数は、反応に関与する分子種の数を示しています。率法、実験的に決定することができますのみ速度定数と反応順序などを知ることが非常に重要です。この実験では、探索率の法律を決定する 1 つの方法、化学反応の進行状況を理解するために使用します。
Principles
Procedure
Results
Oxygen Evolution Data and Initial Rates

Figure 1. Pressure vs. time data for each trial at constant temperature. The slope is equivalent to the instantaneous rate of the reaction.
Reaction Order
- Data for five trials and graph with slope is tabulated below (Table 2, Figure 2). The slope of 0.9353 ≈ 1, is an integer value of the reaction order.

Table 2. Results from 5 H2O2 trials.

Figure 2. Natural log plot of concentration vs. rate. The slope is equivalent to the order of the reaction.
Rate Constant, k
- Calculate the rate in mol O2/s using the Ideal Gas law by first subtracting out the vapor pressure of water at 294 K (temperature of the kinetics experiment), 18.7 torr.
- Calculate the rate constant by dividing the rate, [H2O2]/s by the initial concentration of [H2O2]0.

Table 3. Calculation of the rate constant, k.
- The average rate constant, 2.25 x 10-4 s-1 indicates the reaction is first order based on the units. The rate law could be rewritten as: rate = 2.25 x 10-4 s-1[H2O2]0
Applications and Summary
While determining rate law variables can be involved mathematically, the methods are actually quite straightforward. As long as the disappearance of a reactant or appearance of a product can be measured, rate plots can used to calculate the rate constant. An extension of this method is frequently used to determine the activation energy of a reaction, Ea, by measuring the rate and calculating the rate constant at a variety of temperatures. This method involves using the Arrhenius equation, k = Ae(-Ea/RT). Combining the rate law, including reaction order, with the activation energy of a reaction provides a full kinetic profile for how fast (or slow) a reaction progresses and provides real-world information on how factors like temperature and concentration can affect that reaction.
Chemical kinetics find applications in industries and fields as varied as pharmaceuticals, nuclear safety, environmental remediation, and sunscreens. For example, a certain drug may have a very large rate constant, meaning it decays very quickly in the body. This affects usage, dosing, and delivery method. With respect to nuclear science, radioactivity follows first-order kinetics, meaning that the time required for nuclear material to decay to a safe level is very well characterized. Measurements would be very similar to the method presented here and could also be applied to the decay of many environmental pollutants. Similarly, sunscreens also decay with known kinetic profiles allowing manufacturers to inform consumers how soon the sunscreen needs to be applied to maintain safe levels.
References
- Method adapted from Vetter, T. A., Colombo, D. P. Jr. Kinetics of Platinum-Catalyzed Decomposition of Hydrogen Peroxide, J. Chem. Ed. 80 (7), 788-798 (2003).
- David R. Lide, ed. CRC Handbook of Chemistry and Physics. Boca Raton, Florida: CRC Press (2005).
Transcript
All chemical reactions have a specific rate, which defines how quickly the reactants turn into products.
Chemical reactions are governed by two factors: kinetics and thermodynamics. Thermodynamic factors account for whether or not a reaction will occur, and if it absorbs or gives off energy during the process.
Kinetics refers to the rate of a chemical reaction, and how fast the system reaches equilibrium. The kinetics of a reaction is described by the kinetic rate law, which defines the rate based on a reaction rate constant, the concentration of components, and the order of the reaction.
This video will introduce reaction kinetics using the rate law equation, and will demonstrate how to determine the rate law for a certain reaction in the laboratory.
For a general reaction, the reaction rate equals the rate constant times the concentrations of the reactants, each raised to a reaction order. The rate constant, k, is fixed for a reaction at a given temperature.
The reaction orders are independent of the stoichiometric coefficients. Instead they are dependent on the reaction mechanism, and illustrate how the rate is related to the concentration of reactants. For example, if the reaction rate is unchanged when the concentration of “A” doubles, then the reaction does not depend on concentration, and the order is zero.
If the rate doubles when the concentration of reactant “A” doubles, then the reaction is first order with respect to “A.” The same behavior is true for reactant “B”. The overall order of a reaction is the sum of the individual reaction orders for each reactant.
During a reaction, the concentration of reactants changes with time. Note that that the basic rate equation does not include time as a variable, and can only relate rate and concentration at a specific time point. However, the rate changes as the reaction proceeds and as reactants are depleted. Using a differential rate law can relate the change in concentration to time.
The rate law for a reaction must be determined experimentally, where a chemical reaction is carefully controlled at a constant temperature, and the concentration of the reactants or products measured at specific time intervals. Since concentration measurements are made at discrete time points, the differential rate law is difficult to correlate to experimental data.
Integrating the differential rate law results in a simpler equation, called the integrated rate law. The integrated rate law compares the reactant concentrations at the start of the reaction and at a specified time.
The integrated rate law equation varies depending on the order of the reaction. These equations can take the linear form y=mx+b. Thus, a plot of concentration vs time yields a linear plot for a zero order equation, a plot of the natural log of concentration vs time yields a linear plot for a first order equation, and so on. By fitting experimental data to these equations, the order of a reaction can be easily determined. The rate constant, k, can then be determined using the slope of the line. Finally, the units of k vary depending on the order of the reaction. For a zero order reaction, the units are moles per liter per second, for a first order reaction, the units are inverse seconds and for a second order reaction the units are liter per mole per second.
Now that the basics of kinetic rate laws have been explained, lets take a look at how to experimentally determine the rate law for the decomposition of hydrogen peroxide to water and oxygen.
In this experiment, the catalytic decomposition of hydrogen peroxide over a platinum catalyst is explored.
First, prepare 5 dilutions of hydrogen peroxide, as shown in the table. In this case, concentrations range from 0.882 – 0.176 M, using a 3% or 0.882 M stock solution. Allow the solutions to equilibrate to room temperature.
Next, prepare the reaction vessel using a test tube. First determine the volume by filling a large test tube to the top with water. Then, insert a 1-hole rubber stopper until it is tight and water pushes out of the hole through the top.
Remove the stopper, and pour the water into a graduated cylinder to measure the exact volume. This is the volume of the reaction vessel.
Next, pour 50 mL of the first hydrogen peroxide solution into the test tube, and then place the tube in the 25 °C water bath. Once equilibrated, add a platinum coated reaction disc, and seal the system with a stopper connected to a gas pressure sensor.
Since one of the products is oxygen gas, the increase of pressure in the system is used to measure the increase in oxygen. Set up the pressure sensor to acquire data at 2 points per s, then run the experiment for 120 s. Bubbles should be visible as the peroxide decomposes to oxygen gas and water.
When the reaction period is over, release the pressure and dispose of the peroxide solution. Rinse the tube, then fill the tube with the next hydrogen peroxide solution. Repeat the gas pressure measurement for all solutions.
Plot the pressure versus time data for each solution. The pressure of evolved oxygen is directly proportional to the moles of oxygen formed according to the ideal gas law. Following the chemical reaction, the moles of oxygen formed can be used to calculate the moles of decomposed hydrogen peroxide. First, assume that the concentration of hydrogen peroxide did not change significantly during the short duration of the experiment. Thus, the plotted data represents only the initial region of the kinetics experiment.
Determine the slope of each data set using a linear regression. The slope is equal to the initial reaction rate in units of pressure of oxygen per second.
Next, plot of the natural log of the initial reaction rate vs the natural log of initial peroxide concentration. The slope is equal to the reaction order, m, and is approximately equal to one. Therefore, the reaction is first order.
The rate for each trial is in units of pressure in Torr, per second. To determine the rate constant, first convert the rate to units of atmospheres per second. Because the bubbles evolved in the aqueous solution, subtract the vapor pressure of water from the system pressure for each trial. The new rate then only reflects the pressure due to oxygen evolution.
Apply the ideal gas law to convert the rate from atmospheres per se to moles per s for each trial. Two times the moles of oxygen produced are equal to the moles of hydrogen peroxide decomposed, according to the chemical reaction stoichiometry. Then, use the reaction volume to convert the units of the rate to molarity per second.
Determine the rate constants for each trial by dividing the rate in molarity per s by the initial concentration. In this experiment, the average rate constant, k, is approximately 1.48 x 10-4 per s. The reaction is first order, known from the natural log – natural log plot shown earlier. Therefore, the rate law can be written as shown.
Now that you’ve looked at how to determine the rate law for a chemical reaction, lets look at some areas where this concept is applied.
Chemical reactions are used in the synthesis of compounds and materials used in a wide range of scientific applications. It is important to understand the reaction rate in these synthesis steps, in order to control the progress of a reaction.
For example, the synthesis of cadmium selenide nanocrystals and nanorods proceeds through a series of chemical reactions. Each reaction has its own discrete reaction rate, and therefore synthesis step is carefully controlled based on the knowledge speed of the reaction; some slow and some very quick.
The reaction rate law can also be used to describe radioactive decay, and determine the half-life of radioactive material. Half-life refers to the amount of time required for the concentration of a material to fall to half of its initial concentration.
Radioactivity follows first order kinetics, meaning that the time required for radioactive material to decay to a safe level can be very well characterized, enabling proper transport and storage of radioactive material and radioactive waste.
Similar to radioactive materials, drugs also have a half-life and degrade in the body. For example, some drugs have high rate constants, meaning that they degrade quickly, and must be taken frequently. Knowledge of this degradation rate enables the determination of the appropriate dosage, usage and delivery method.
You’ve just watched JoVE’s introduction to reaction rates. You should now understand the different orders of chemical reactions, how they relate to chemical reaction rates, and how to determine the rate law for a given chemical reaction in the laboratory.
Thanks for watching!
