Overview
Fonte: Tamara M. Powers, Dipartimento di Chimica, Texas A & M University
Mentre la maggior parte delle molecole organiche sono diamagnetiche, in cui tutti i loro elettroni sono accoppiati in legami, molti complessi di metalli di transizione sono paramagnetici, che ha stati di base con elettroni spaiati. Ricordiamo la regola di Hund, che afferma che per orbitali di energie simili, gli elettroni riempiranno gli orbitali per massimizzare il numero di elettroni spaiati prima di accoppiarsi. I metalli di transizione hanno orbitali dparzialmente popolati le cui energie sono perturbate in misura variabile dalla coordinazione dei ligandi al metallo. Quindi, gli orbitali dsono simili in energia l'uno all'altro, ma non sono tutti degenerati. Ciò consente ai complessi di essere diamagnetici, con tutti gli elettroni accoppiati, o paramagnetici, con elettroni spaiati.
Conoscere il numero di elettroni spaiati in un complesso metallico può fornire indizi sullo stato di ossidazione e sulla geometria del complesso metallico, nonché sulla forza del campo del ligando (campo cristallino) dei ligandi. Queste proprietà hanno un grande impatto sulla spettroscopia e sulla reattività dei complessi di metalli di transizione, e quindi sono importanti da capire.
Un modo per contare il numero di elettroni spaiati è misurare la suscettibilità magnetica, χ, del composto di coordinazione. La suscettibilità magnetica è la misura della magnetizzazione di un materiale (o composto) quando viene inserito in un campo magnetico applicato. Gli elettroni accoppiati sono leggermente respinti da un campo magnetico applicato e questa repulsione aumenta linearmente all'aumentare della forza del campo magnetico. D'altra parte, gli elettroni spaiati sono attratti (in misura maggiore) da un campo magnetico e l'attrazione aumenta linearmente con l'intensità del campo magnetico. Pertanto, qualsiasi composto con elettroni spaiati sarà attratto da un campo magnetico. 1
Quando misuriamo la suscettibilità magnetica, otteniamo informazioni sul numero di elettroni spaiati dal momento magnetico, μ. La suscettibilità magnetica è correlata al momento magnetico, μ dall'equazione 12:
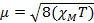 (1)
(1)
La costante 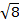 = [(3kB)/Nβ2)], dove β= magnetone di Bohr dell'elettrone (0,93 x 10-20 erg gauss-1), N = numero di Avogadro, e kB = costante di Boltzmann
= [(3kB)/Nβ2)], dove β= magnetone di Bohr dell'elettrone (0,93 x 10-20 erg gauss-1), N = numero di Avogadro, e kB = costante di Boltzmann
XM= suscettibilità magnetica molare (cm3/mol)
T = temperatura (K)
μ = momento magnetico, misurato in unità di magnetone di Bohr, μB = 9,27 x 10-24 JT-1
Il momento magnetico per i complessi è dato dall'equazione 21:
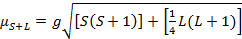 (2)
(2)
g = rapporto giromagnetico = 2,00023 μB
S = numero quantico di spin = ∑ms = [numero di elettroni spaiati, n]/2
L = numero quantico orbitale = ∑ml
Questa equazione ha sia contributi orbitali che di spin. Per i complessi di metalli di transizione di prima fila, il contributo orbitale è piccolo e quindi può essere omesso, quindi il momento magnetico di solo spin è dato dall'equazione 3:
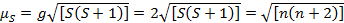 (3)
(3)
Il momento magnetico di sola spin può quindi dare direttamente il numero di elettroni spaiati. Questa approssimazione può essere fatta anche per i metalli più pesanti, sebbene i contributi orbitali possano essere significativi per i metalli di transizione di seconda e terza fila. Questo contributo può essere così significativo da gonfiare il momento magnetico abbastanza che il composto sembra avere più elettroni spaiati di quanti ne abbia. Pertanto, potrebbe essere necessaria un'ulteriore caratterizzazione per questi complessi.
In questo esperimento, il momento magnetico della soluzione di tris(acetilacetonato)ferro(III) (Fe(acac)3) viene determinato sperimentalmente usando il metodo evans nel cloroformio.
Principles
Esistono molti metodi per misurare la suscettibilità magnetica. Alla fine del 19° secolo, Louis Georges Gouy sviluppò la bilancia Gouy, che è un metodo altamente accurato per misurare la suscettibilità magnetica. In questo approccio, una bilancia analitica viene utilizzata per ammassare un magnete e la variazione di massa osservata posizionando un campione paramagnetico tra i poli del magnete è correlata alla suscettibilità magnetica. Questo metodo non è pratico, in quanto sospendere il campione tra i poli del magnete non è banale. Ciò richiede quattro misurazioni di massa tra le quali il magnete non può muoversi e, per i campioni sensibili all'aria, questa misurazione deve essere condotta all'interno di un glovebox. Sono disponibili bilance di suscettibilità magnetica più moderne, ma ciò richiede l'acquisto di tale bilancia.
Un altro metodo consiste nell'utilizzare un magnetometro SQUID (Superconducting Quantum Interference Device). Ciò richiede diversi mg di campione solido e, a meno che non vengano eseguite altre misurazioni magnetiche sul campione, non è pratico o conveniente per i complessi paramagnetici che possono essere trasformati in soluzioni.
Infine, e ciò che sarà dimostrato qui, è l'uso di uno spettrometro NMR per misurare la suscettibilità magnetica. Questo approccio è stato sviluppato da Dennis Evans nel 1959. È semplice e si basa sull'effetto che un paramagnete in soluzione ha sullo spostamento chimico di un composto di riferimento, di solito il solvente. La raccolta dei dati può essere effettuata su qualsiasi spettrometro NMR, i dati sono facili da interpretare e la preparazione del campione è semplice e richiede poco materiale. È diventato il metodo standard per ottenere dati di suscettibilità magnetica per complessi inorganici.
La misurazione della suscettibilità magnetica con il metodo Evans si basa sul fatto che gli elettroni spaiati dal paramagnete in soluzione comporteranno un cambiamento dello spostamento chimico di tutte le specie in soluzione (Figura 1). Pertanto, notando la differenza di spostamento chimico di una molecola di solvente in presenza e assenza di una specie paramagnetica, la suscettibilità magnetica può essere ottenuta tramite l'equazione 4 (per uno spettrometro NMR ad alto campo)3
 (4)
(4)
Δf = differenza di frequenza in Hz tra la risonanza spostata e la risonanza del solvente puro
F = spettrometro a radiofrequenza in Hz
c = concentrazione di specie paramagnetiche (mol/mL)
I dati sono facilmente ottenibili raccogliendo uno spettro NMR di 1H di un campione che contiene un capillare di solvente puro, con una soluzione del paramagnete che circonda il capillare all'interno del tubo NMR (Figura 2).

Figura 1. Esempio 1H spettro NMR dell'esperimento

Figura 2. Immagine di un capillare nella configurazione del tubo NMR
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Preparazione dell'inserto capillare
- Usando un accendino o un'altra fiamma a gas, sciogliere la punta di una lunga pipetta Pasteur. Ruotare delicatamente la punta della pipetta nella fiamma fino a formare una piccola lampadina. Lasciare raffreddare il bicchiere.
- In un flaconcino a scintillazione, preparare una soluzione 50:1 (volume) di cloroformio deuterato:proteo. Pipettare 2 mL di solvente deerato, e a questo aggiungere 40 μL di solvente proteo. Chiudere il flaconcino.
- Aggiungere con attenzione alcune gocce della miscela di solventi alla pipetta di vetro sigillata. Far scorrere delicatamente la punta della pipetta sigillata in modo che il liquido entri nel capillare. Ripetere fino a quando la soluzione ha una profondità di ~ 2 pollici dal fondo del capillare. Assicurati che non ci siano bolle d'aria.
- Tappare la pipetta con un setto di gomma 14/20. Utilizzando una siringa da 3 mL ricoperta da un ago, inserire l'ago nella pipetta ed estrarre 3 ml di aria. Questo crea un vuoto parziale, facilitando il passaggio successivo.
- Sigillare la parte superiore del capillare. Bloccare orizzontalmente la pipetta a un supporto ad anello. Utilizzare un accendino per ammorbidire il vetro sopra la soluzione nella parte inferiore della pipetta. Una volta che il vetro si ammorbidisce, iniziare a ruotare la punta della pipetta e tirare la punta della pipetta lontano dalla base bloccata. Lasciare raffreddare il capillare sigillato.
2. Preparazione della soluzione paramagnetica
- Utilizzando una bilancia analitica, massa una fiala a scintillazione e coperchio. Nota la massa.
- Massa 5-10 mg di Fe(acac)3 nella fiala di scintillazione e notare la massa. Fe(acac)3 ha un momento magnetico di soluzione molto elevato. Pertanto 5-10 mg genereranno un grande cambiamento dello spostamento chimico. In genere, 10 - 15 mg è una massa più appropriata da utilizzare per i campioni del metodo Evans.
- Pipettare ~ 600 μL della miscela di solvente preparata nel flaconcino contenente le specie paramagnetiche. Tappare la fiala e annotare la massa. Assicurarsi che il solido si dissolva completamente.
3. Preparazione del campione NMR
- In un tubo NMR standard, far cadere con attenzione l'inserto capillare ad angolo, per assicurarsi che non lo rompa.
- Pipetta nella soluzione contenente le specie paramagnetiche.
- Tappare il tubo NMR. Per i campioni sensibili all'aria, avvolgere Parafilm attorno al cappuccio.
4. Raccolta dei dati
- Acquisire e salvare uno spettro NMR standard da 1ora.
- Nota la temperatura della sonda.
- Notare la radiofrequenza.
5. Analisi dei dati e risultati
- Utilizzando la massa e la densità del solvente, calcolare il volume del solvente utilizzato per preparare la soluzione paramagnetica.
- Calcolare la concentrazione (M) della soluzione paramagnetica.
- Calcolare la separazione di picco della risonanza del solvente tra quella del solvente puro (nel capillare) e quella spostata dal paramagnete (al di fuori del capillare) (Δppm). Se questo viene fatto in ppm, convertirlo in Hz con l'equazione 5:
 (5)
(5)
F = spettrometro a radiofrequenza in Hz - Calcola la suscettibilità magnetica usando l'equazione 4.
- Calcola il momento magnetico usando l'equazione 1.
- Confronta il momento magnetico ottenuto con quello previsto per n elettroni spaiati dall'equazione 3. La suscettibilità magnetica sarà leggermente maggiore del valore di solo spin previsto indicato nella tabella, ma dovrebbe essere inferiore a quella che corrisponde a n+1 elettroni spaiati.
- Dare il numero di elettroni spaiati per le specie paramagnetiche.
6. Risoluzione dei problemi
- Se non si osservano due picchi di solvente ben risolti, provare quanto segue:
- Utilizzare uno spettrometro con una maggiore intensità di campo per aumentare la differenza di spostamento chimico (in ppm) dei due picchi.
- Rendere il campione più concentrato, in modo che lo spostamento sia più grande.
- A volte il valore non ha senso. Se si ottiene un valore troppo basso, provare a eseguire le operazioni seguenti:
- Ripetere, facendo maggiore attenzione nel massare le specie solventi e paramagnetiche.
- Assicurarsi che la specie paramagnetica utilizzata sia pura. Anche le impurità del solvente nei cristalli influenzeranno la massa e quindi la concentrazione.
- Per le molecole di grandi dimensioni, il diamagnetismo può essere così significativo che deve essere effettuata una correzione diamagnetica. Questo termine viene sottratto all'equazione 4:

- A volte il valore non ha senso. Se si ottiene un valore troppo alto, provare a eseguire le operazioni seguenti:
- Seguire gli stessi passaggi di 6.2.1-6.2.3.
- Per i metalli più pesanti, può essere necessario includere contributi orbitali.
7. Campioni sensibili all'aria
- I campioni sensibili all'aria possono essere facilmente analizzati utilizzando questa tecnica. I passaggi 1.2-1.4, 2 e 3 vengono semplicemente eseguiti all'interno di un vano portaoggetti.
Il metodo Evans è una tecnica per calcolare il numero di elettroni spaiati in complessi metallici allo stato di soluzione.
Molti complessi di metalli di transizione hanno elettroni spaiati, che li rendono attratti dai campi magnetici. Questi complessi sono chiamati paramagnetici. I complessi con tutti gli elettroni accoppiati sono chiamati diamagnetici.
Conoscere il numero di elettroni spaiati è importante per prevedere la reattività di un composto. Il metodo Evans utilizza la spettroscopia NMR per misurare i parametri necessari per calcolare il numero di elettroni spaiati.
Questo video illustrerà la procedura per eseguire il metodo Evans, dimostrerà l'analisi di Fe(acac)3e introdurrà alcune applicazioni del conteggio degli elettroni spaiati in chimica.
Il numero di elettroni spaiati in un complesso può essere determinato dal momento magnetico della molecola data. I momenti magnetici dei complessi di metalli di transizione di1a fila possono essere approssimati dai contributi di elettroni spaiati, chiamati momento magnetico di sola spin. Per i complessi di metalli di transizione di2a e3a fila, devono essere considerati sia i contributi di spin che quelli orbitali.
Il momento magnetico è correlato alla suscettibilità magnetica, che fornisce il grado di magnetizzazione di un complesso in un campo magnetico applicato.
Lo spostamento chimico di una specie in uno spettro NMR è influenzato dalla suscettibilità magnetica complessiva della soluzione campione. Pertanto, lo spostamento chimico di un solvente cambia se il soluto è paramagnetico. Il metodo evans utilizza questa relazione per ottenere la suscettibilità magnetica, e quindi il momento magnetico, di quel soluto paramagnetico.
Un campione del metodo Evans utilizza un inserto capillare contenente una miscela di un solvente deuterato e il solvente proteato corrispondente. Il composto di interesse viene disciolto nella stessa miscela di solventi e posto in un tubo NMR con il capillare.
Lo spettro NMR acquisito mostra due picchi di solvente: uno corrispondente al solvente proteato in soluzione con il composto e l'altro corrispondente al solvente proteato nel capillare.
La suscettibilità magnetica è calcolata dalla differenza di frequenza e dalla concentrazione del composto paramagnetico nel campione.
Il momento magnetico è calcolato dalla suscettibilità magnetica in un'unità speciale chiamata magnetone di Bohr. Il momento magnetico può quindi essere confrontato con i valori teorici di solo spin per stimare il numero di elettroni spaiati nel campione.
Ora che hai compreso i principi del metodo Evans, passiamo attraverso una procedura per trovare il numero di elettroni spaiati in Fe(acac)3 con il metodo Evans.
Per preparare l'inserto capillare, sciogliere la punta di una lunga pipetta Pasteur con una fiamma fino a quando la punta si scioglie in una lampadina di vetro. Lasciare raffreddare il bicchiere.
Quindi, combinare in un flaconcino a scintillazione pulita 2 mL di un solvente deuterato e 40 μL di un solvente proteato. Tappare il flaconcino e ruotare delicatamente.
Aggiungere con attenzione alcune gocce della miscela di solventi alla pipetta raffreddata. Far scorrere delicatamente o picchiettare la punta della pipetta fino a quando il solvente non si è raccolto nella parte inferiore della punta.
Continuare ad aggiungere la miscela di solventi in questo modo fino a quando la soluzione riempie la punta della pipetta sigillata ad una profondità di circa 2 pollici, senza bolle d'aria.
Tappare la pipetta con un setto di gomma 14/20. Equipaggiare una siringa da 3 ml con un ago. Inserire l'ago attraverso il setto e prelevare con attenzione 3 ml di aria.
Rimuovere la siringa e bloccare la pipetta su un supporto ad anello orizzontalmente. Utilizzare un accendino per ammorbidire il vetro sopra la soluzione nella punta della pipetta.
Una volta che il vetro inizia ad ammorbidirsi, ruotare lentamente la punta della pipetta riempita di soluzione per sigillare la soluzione. Continuare a ruotare il capillare appena formato fino a quando non si separa facilmente dal corpo della pipetta.
Lasciare raffreddare l'inserto capillare e quindi conservarlo in un contenitore etichettato.
Per preparare un campione per il metodo Evans, registrare prima la massa di una fiala e di un cappuccio a scintillazione. Quindi, posizionare 5 mg del composto paramagnetico di interesse nella fiala di scintillazione e registrare la massa.
Pipettare circa 600 μL della miscela di solventi deuterati e proteati nel flaconcino di scintillazione. Ruotare il flaconcino fino a quando il composto solido si dissolve completamente.
Registrare la massa del flaconcino limitato della soluzione campione. Quindi, ottenere un tubo e un cappuccio NMR standard.
Far scorrere con attenzione l'inserto capillare nel tubo NMR ad angolo. Trasferire la soluzione del composto paramagnetico al tubo NMR e tappare il tubo. Assicurarsi che l'inserto si trova nella parte inferiore del tubo.
Acquisire e salvare uno spettro NMR standard da 1ora.
Innanzitutto, calcolare la concentrazione della soluzione campione in moli per centimetro cubo utilizzando le masse registrate e la densità del solvente. Quindi, convertire la differenza tra gli spostamenti chimici del picco del solvente da ppm a Hz. Calcolare la suscettibilità magnetica molare del campione.
Quindi, calcolare il momento magnetico dalla temperatura della sonda e la suscettibilità magnetica molare. Confrontare il valore calcolato con una tabella di valori noti per determinare il numero di elettroni spaiati nel composto.
Il numero di elettroni spaiati è importante per la modellazione di complessi chimici e biologici. Diamo un'occhiata ad alcune applicazioni.
I complessi di metalli di transizione possono essere modellati con la teoria orbitale molecolare. In questo modello, gli elettroni sono assegnati agli orbitali molecolari condivisi tra gli atomi. Le informazioni sul numero di elettroni spaiati aiutano a confermare che viene utilizzato un modello appropriato. Inoltre, il numero di orbitali occupati e non occupati da solo predice come il complesso reagirà con altre molecole.
Le molecole possono essere classificate in base alle operazioni di simmetria che possono eseguire, come essere specchiate su un asse. La simmetria molecolare può prevedere molte proprietà, come le modalità vibrazionali di un composto. Poiché il numero di elettroni spaiati può fornire informazioni sulla geometria molecolare, è importante determinare con precisione il numero di elettroni spaiati quando si caratterizzano i composti.
Hai appena visto l'introduzione di JoVE al metodo Evans. Ora dovresti capire i principi alla base del metodo Evans, la procedura per calcolare il numero di elettroni spaiati e come gli elettroni spaiati sono rilevanti per comprendere la reattività chimica. Grazie per l'attenzione!
Subscription Required. Please recommend JoVE to your librarian.
Results
Risultatixperimental
| Fe(acac)3 | Cloroformio | |
| m (g) | 0.0051 | 0.874 |
| MW (g/mol) | 353.17 | n/d |
| n (mol) | 1,44⋅10-5 | n/d |
| Densità (g/mL) | n/d | 1.49* |
| Volume (mL) | n/d | 0.587 |
| c (mol/mL) | 2,45⋅10-5 | |
| Turni NMR | Picco 1 | Picco 2 |
| δ (ppm) | 7.26 | 5.85 |
| Δppm | 1.41 | |
| Strumento NMR | ||
| Temperatura (K) | 296.3 | |
| Campo, F (Hz) | 500⋅106 |
* la densità del solvente può essere approssimata alla densità del solvente utilizzato
Calcoli:

 = 0,0137 cm3/mol
= 0,0137 cm3/mol = 5,70 μB
= 5,70 μB
Risultati teorici per dati S e n valori:
| S | n | μS |
| 1/2 | 1 | 1.73 |
| 1 | 2 | 2.83 |
| 3/2 | 3 | 3.87 |
| 2 | 4 | 4.90 |
| 5/2 | 5 | 5.92 |
Per 4,5 mg di Fe(acac)3 disciolto in solvente da 0,58 mL, con uno strumento a 300 MHz si osserva una separazione di picco di 1,41 ppm, che dà XM= 1,37 x 10-2 e μeff = 5,70. Questo μ valoreeff è coerente con un complesso S = 5/2, che ha 5 elettroni spaiati.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
Il metodo Evans è un metodo semplice e pratico per ottenere la suscettibilità magnetica dei complessi metallici solubili. Ciò fornisce il numero di elettroni spaiati in un complesso metallico, che è pertinente alla spettroscopia, alle proprietà magnetiche e alla reattività del complesso.
Misurare la suscettibilità magnetica delle specie paramagnetiche fornisce il numero di elettroni spaiati, che è una proprietà chiave dei complessi metallici. Poiché la reattività dei complessi metallici è influenzata dalla sua struttura elettronica - cioè come sono popolati gli orbitali d - è importante stabilire il numero di elettroni spaiati. La suscettibilità magnetica può essere utilizzata per determinare la geometria del complesso metallico in soluzione, fornire informazioni sull'intensità del campo del ligando e può fornire prove per la corretta assegnazione formale dello stato di ossidazione del complesso metallico. Nei moduli su "Teoria dei gruppi" e "Teoria MO dei complessi di metalli di transizione", introdurremo come prevedere i diagrammi di scissione d-orbitale e come utilizzare i dati del metodo Evans per aiutare a determinare la geometria di un complesso metallico e fornire prove dello stato di ossidazione del centro metallico.
Esistono diversi strumenti che possono essere utilizzati per misurare la suscettibilità magnetica di una specie paramagnetica, tra cui un equilibrio Gouy, uno SQUID o uno strumento NMR. Il metodo Evans è una tecnica semplice e pratica che utilizza la NMR per determinare il momento magnetico di soluzione di un paramagnete. Mentre il metodo Evans è uno strumento potente nel campo del magnetismo, ci sono diversi inconvenienti alla tecnica. In primo luogo, la molecola deve essere solubile nel solvente utilizzato nell'esperimento. Se il campione paramagnetico non è completamente disciolto, la concentrazione della soluzione sarà errata, il che porterà a errori nel momento magnetico della soluzione determinato sperimentalmente. Altri errori di concentrazione possono verificarsi se il campione paramagnetico presenta impurità diamagnetiche (solventi) o paramagnetiche.
Subscription Required. Please recommend JoVE to your librarian.
References
- Miessler, G. L., Fischer, P. J., Tarr, D. A. Inorganic Chemistry. 5 ed. Pearson. (2014).
- Drago, R. S. Physical Methods for Chemists. 2 ed. Saunders College Publishing. (1992).
- Girolami, G. S., Rauchfuss, T. B., Angelici, R. J. Synthesis and Technique in Inorganic Chemistry: A Laboratory Manual. 3 ed. University Science Books. Sausalito, CA, (1999).





 (5)
(5)