Source: Laboratory of Dr. Andreas Züttel - Swiss Federal Laboratories for Materials Science and Technology
The ideal gas law describes the behavior of most common gases at near-ambient conditions and the tendency of all chemical matter in the dilute limit. It is a fundamental relationship between three measurable macroscopic system variables (pressure, temperature, and volume) and the number of molecules of gas in the system, and is therefore an essential link between the microscopic and the macroscopic universes.
The history of the ideal gas law dates to the middle of the 17th century when the relationship between the pressure and volume of air was found to be inversely proportional, an expression confirmed by Robert Boyle and which we now refer to as Boyle’s law (Equation 1).
P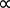 
V-1 (Equation 1)
Unpublished work by Jacques Charles in the 1780s, which was extended to numerous gases and vapors by Joseph Louis Gay-Lussac and reported in 1802, established the directly proportional relationship between the absolute temperature and volume of a gas. This relationship is called Charles's law (Equation 2).
V 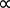T (Equation 2)
Guillaume Amontons is typically credited with first discovering the relationship between the temperature and pressure of air within a fixed volume at the turn of the 18th century. This law was also extended to numerous other gases by Joseph Louis Gay-Lussac at the beginning of the 19th century and is therefore either referred to as either Amontons’s law or Gay-Lussac's law, stated as shown in Equation 3.
P 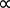T (Equation 3)
Together, these three relationships can be combined to give the relationship in Equation 4.
V 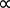T (Equation 4)
Finally, in 1811, it was proposed by Amedeo Avogadro that any two gases, held in the same volume and at the same temperature and pressure, contain the same number of molecules. This led to the conclusion that all gases may be described by a common constant, the ideal gas constant R, that is independent of the nature of the gas. This is known as the ideal gas law (Equation 5).1,2
PV 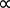T (Equation 5)
1. Measuring the Volume of the Sample
2. Load the Sample in the Balance
3. Measure Sample Weight as a Function of Pressure at Room Temperature
4. Measure Sample Weight as a Function of Pressure at Various Temperatures
5. Calculate the Ideal Gas Constant
(Equation 9)The ideal gas law is a fundamental and useful relationship in science as it describes the behavior of most common gases at near-ambient conditions.
The ideal gas law, PV=nRT, defines the relationship between the number of molecules of gas in a closed system and three measurable system variables: pressure, temperature, and volume.
The ideal gas law relies on several assumptions. First, that the volume of the gas molecules is negligibly small. Second, that the molecules behave as rigid spheres that obey Newton's laws of motion. And finally, that there are no intermolecular attractive forces between the molecules. They only interact with each other through elastic collisions, so there is no net loss in kinetic energy. Gases deviate from this ideal behavior at high pressures, where the gas density increases, and the real volume of the gas molecules becomes important. Similarly, gases deviate at extremely low temperatures, where attractive intermolecular interactions become important. Heavier gases may deviate even at ambient temperature and pressure due to their higher density and stronger intermolecular interactions.
This video will experimentally confirm the ideal gas law by measuring the change in density of a gas as a function of temperature and pressure.
The ideal gas law is derived from four important relationships. First, Boyle's law describes the inversely proportional relationship between the pressure and volume of a gas. Next, Gay-Lussac's law states that temperature and pressure are proportional. Similarly, Charles's law is a statement of the proportionality between temperature and volume. These three relationships form the combined gas law, which enables the comparison of a single gas across many different conditions.
Finally, Avogadro determined that any two gases, held at the same volume, temperature and pressure, contain the same number of molecules. Because gases under the same condition typically behave the same, a constant of proportionality, called the universal gas constant (R), could be found to relate these parameters, enabling the comparison of different gases. R has units of energy per temperature per molecule; for example, joules per kelvin per mole.
The ideal gas law is a valuable tool in understanding state relationships in gaseous systems. For example, in a system of constant temperature and pressure, the addition of more gas molecules results in increased volume.
Similarly, at constant temperature in a closed system, where no molecules are added or subtracted, the pressure of a gas is increased when volume is decreased.
A magnetic suspension balance can be used to confirm the ideal gas law experimentally by measuring the physical properties of a system. The weight of a solid sample of constant mass and volume can serve as a probe of the properties of the gas around it.
As pressure increases in the system, at constant system volume and temperature, the amount of gas molecules in the system increases, thereby increasing the gas density. The rigid solid sample submerged in this gas is subject to buoyancy, and its apparent weight decreases although its mass is unchanged. The change in gas density can be determined because of Archimedes principle, which states that the change in object weight is equal to the change in weight of the gas that is displaced.
The precise behaviors of the gas density under different pressure and temperature conditions will correspond to the ideal gas law if the previously described approximations hold true, enabling the straightforward calculation of the universal gas constant, R.
In the following series of experiments, a microbalance will be used to confirm the ideal gas law and determine the universal gas constant, R, by measuring the density of hydrogen as a function of temperature and pressure. First, carefully clean the sample, in this case a finely machined aluminum block, with acetone, and dry. Measure the volume of the sample by filling a graduated cylinder with enough distilled water to cover the sample. Note the initial volume. Immerse the sample in the water, and note the volume change.
Remove and carefully clean and dry the sample. Next, load it into the magnetic suspension balance, in this case located inside of a glove box. Install the pressure-temperature chamber around the sample. The sample is now magnetically suspended in a closed system, not touching any of the walls.
Evacuate the sample environment and refill with hydrogen gas, to a pressure of 1 bar.
Measure the sample weight, and label it as the initial weight at room temperature. Next, increase the pressure in the sample environment to 2 bar, and allow it to equilibrate. Measure the weight at the new pressure. Repeat these steps several times at a number of pressures, to acquire a series of sample weights at corresponding pressures, all at room temperature.
Next, measure weight as a function of pressure at a higher temperature. First evacuate the sample environment, then increase the temperature to 150 °C and allow it to equilibrate. Then, increase the pressure to 1 bar. Measure the sample weight, and label it as the initial weight at 150 °C and 1 bar. Increase the pressure, allow it to equilibrate, and measure the weight. Repeat these steps in order to measure a series of sample weights at a range of pressures. To obtain more data, repeat the series of weight measurements at other constant temperatures and pressures.
To calculate the ideal gas constant, tabulate the measured values of sample weight at each temperature and pressure.
Next, calculate the differences between all pairs of sample weights within a single temperature set to obtain all possible combinations of the change in weight as a function of change in pressure, or Δw. This change is equivalent to the change in weight of the hydrogen gas that is displaced by the sample.
Similarly, calculate all corresponding differences in pressure to obtain change in pressure, or ΔP. Tabulate all pairs of changes in weight and pressure for each temperature. Convert the units of temperature to kelvin and the units of pressure to pascals.
Since the volume and temperature remain constant for each series of measurements, the ideal gas law can be written as ΔPV=ΔnRT. Since Δn is equal to Δw divided by the molecular weight of hydrogen, calculate each value of Δn for each value of Δw.
Plot the product of pressure change and sample volume, as a function of the product of Δn and temperature. Perform a linear regression analysis to determine the slope, which will equal the universal gas constant if done correctly.
The ideal gas equation is used in many real world scenarios, typically those performed with gases at ambient temperature and pressure. All gases deviate from ideal behavior at high pressure; however, some gases, such as carbon dioxide, deviate more than others. In this experiment, deviations from ideal behavior were measured for carbon dioxide gas. The procedure was identical to the previous experiment conducted with hydrogen.
A plot of pressure times volume versus moles times temperature was plotted, and the ideal gas constant calculated from the slope of the plot. Carbon dioxide deviated significantly from ideal behavior, even at ambient conditions. This behavior was caused by attractive intermolecular interactions, which was not observed with hydrogen.
The ideal gas law is used in the identification and quantification of explosive gases in air samples. This research area is of extreme importance to the military and security.
Here, explosive components of a gas sample were quantified using temperature desorption gas chromatography. The data, as well as the ideal gas law were then used to quantify these dangerous substances.
You've just watched JoVE's Introduction to the ideal gas law. After watching this video, you should understand the concept of the law, and situations where the equation is applicable.
Thanks for watching!
The ideal gas law is a fundamental and useful relationship in science?as it describes the behavior of most common gases at near-ambient conditions.
The ideal gas law, PV=nRT, defines the relationship between the number of molecules of gas in a closed system and three measurable system variables: pressure, temperature, and volume.
The ideal gas law relies on several assumptions. First, that the volume of the gas molecules is negligibly small. Second, that the molecules behave as rigid spheres that obey Newton's laws of motion. And finally, that there are no intermolecular attractive forces between the molecules. They only interact with each other through elastic collisions, so there is no net loss in kinetic energy. Gases deviate from this ideal behavior at high pressures, where the gas density increases, and the real volume of the gas molecules becomes important. Similarly, gases deviate at extremely low temperatures, where attractive intermolecular interactions become important. Heavier gases may deviate even at ambient temperature and pressure due to their higher density and stronger intermolecular interactions.
This video will experimentally confirm the ideal gas law by measuring the change in density of a gas as a function of temperature and pressure.
The ideal gas law is derived from four important relationships. First, Boyle's law describes the inversely proportional relationship between the pressure and volume of a gas. Next, Gay-Lussac's law states that temperature and pressure are proportional. Similarly, Charles's law is a statement of the proportionality between temperature and volume. These three relationships form the combined gas law, which enables the comparison of a single gas across many different conditions.
Finally, Avogadro determined that any two gases, held at the same volume, temperature and pressure, contain the same number of molecules. Because gases under the same condition typically behave the same, a constant of proportionality, called the universal gas constant?(R), could be found to relate these parameters, enabling the comparison of different gases. R has units of energy per temperature per molecule;?for example, joules per kelvin per mole.
The ideal gas law is a valuable tool in understanding state relationships in gaseous systems. For example, in a system of constant temperature and pressure, the addition of more gas molecules results in increased volume.
Similarly, at constant temperature in a closed system, where no molecules are added or subtracted, the pressure of a gas is increased when volume is decreased.
A magnetic suspension balance can be used to confirm the ideal gas law experimentally by measuring the physical properties of a system. The weight of a solid sample of constant mass and volume can serve as a probe of the properties of the gas around it.
As pressure increases in the system, at constant system volume and temperature, the amount of gas molecules in the system increases, thereby increasing the gas density. The rigid solid sample submerged in this gas is subject to buoyancy, and its apparent weight decreases although its mass is unchanged. The change in gas density can be determined because of Archimedes principle, which states that the change in object weight is equal to the change in weight of the gas that is displaced.
The precise behaviors of the gas density under different pressure and temperature conditions will correspond to the ideal gas law if the previously described approximations hold true, enabling the straightforward calculation of the universal gas constant, R.
In the following series of experiments, a microbalance will be used to confirm the ideal gas law and determine the universal gas constant, R, by measuring the density of hydrogen as a function of temperature and pressure. First, carefully clean the sample, in this case a finely machined aluminum block, with acetone, and dry. Measure the volume of the sample by filling a graduated cylinder with enough distilled water to cover the sample. Note the initial volume. Immerse the sample in the water, and note the volume change.
Remove and carefully clean and dry the sample. Next, load it into the magnetic suspension balance, in this case located inside of a glove box. Install the pressure-temperature chamber around the sample. The sample is now magnetically suspended in a closed system, not touching any of the walls.
Evacuate the sample environment and refill with hydrogen gas, to a pressure of 1 bar.
Measure the sample weight, and label it as the initial weight at room temperature. Next, increase the pressure in the sample environment to 2 bar, and allow it to equilibrate. Measure the weight at the new pressure. Repeat these steps several times at a number of pressures, to acquire a series of sample weights at corresponding pressures, all at room temperature.
Next, measure weight as a function of pressure at a higher temperature. First evacuate the sample environment, then increase the temperature to 150 ?C and allow it to equilibrate. Then, increase the pressure to 1 bar. Measure the sample weight, and label it as the initial weight at 150 ?C and 1 bar. Increase the pressure, allow it to equilibrate, and measure the weight. Repeat these steps in order to measure a series of sample weights at a range of pressures. To obtain more data, repeat the series of weight measurements at other constant temperatures and pressures.
To calculate the ideal gas constant, tabulate the measured values of sample weight at each temperature and pressure.
Next, calculate the differences between all pairs of sample weights within a single temperature set to obtain all possible combinations of the change in weight as a function of change in pressure, or ?w. This change is equivalent to the change in weight of the hydrogen gas that is displaced by the sample.
Similarly, calculate all corresponding differences in pressure to obtain change in pressure, or ?P. Tabulate all pairs of changes in weight and pressure for each temperature. Convert the units of temperature to kelvin and the units of pressure to pascals.
Since the volume and temperature remain constant for each series of measurements, the ideal gas law can be written as ?PV=?nRT. Since ?n is equal to ?w divided by the molecular weight of hydrogen, calculate each value of ?n for each value of ?w.
Plot the product of pressure change and sample volume, as a function of the product of ?n and temperature. Perform a linear regression analysis to determine the slope, which will equal the universal gas constant if?done correctly.
The ideal gas equation is used in many real world scenarios, typically those performed with gases at ambient temperature and pressure. All gases deviate from ideal behavior at high pressure;?however, some gases, such as carbon dioxide, deviate more than others. In this experiment, deviations from ideal behavior were measured for carbon dioxide gas. The procedure was identical to the previous experiment conducted with hydrogen.
A plot of pressure times volume versus moles times temperature was plotted, and the ideal gas constant calculated from the slope of the plot. Carbon dioxide deviated significantly from ideal behavior, even at ambient conditions. This behavior was caused by attractive intermolecular interactions, which was not observed with hydrogen.
The ideal gas law is used in the identification and quantification of explosive gases in air samples. This research area is of extreme importance to the military and security.
Here, explosive components of a gas sample were quantified using temperature desorption gas chromatography. The data, as well as the ideal gas law were then used to quantify these dangerous substances.
You've just watched JoVE's Introduction to the ideal gas law. After watching this video, you should understand the concept of the law, and situations where the equation is applicable.
Thanks for watching!
09:52
General Chemistry
706.7K Views
09:49
General Chemistry
290.3K Views
07:19
General Chemistry
599.4K Views
07:30
General Chemistry
389.2K Views
07:05
General Chemistry
195.2K Views
09:09
General Chemistry
151.2K Views
09:28
General Chemistry
360.1K Views
10:17
General Chemistry
449.7K Views
09:03
General Chemistry
168.3K Views
08:37
General Chemistry
273.7K Views
08:53
General Chemistry
165.7K Views
10:49
General Chemistry
202.4K Views
11:14
General Chemistry
47.1K Views
08:42
General Chemistry
96.4K Views
