焓值

化学家通常使用称为焓（ H ）的属性来描述化学过程和物理过程的热力学。焓定义为系统内部能量（ E ）与其压力（ P ）和体积（ V 的数学乘积之和>）：

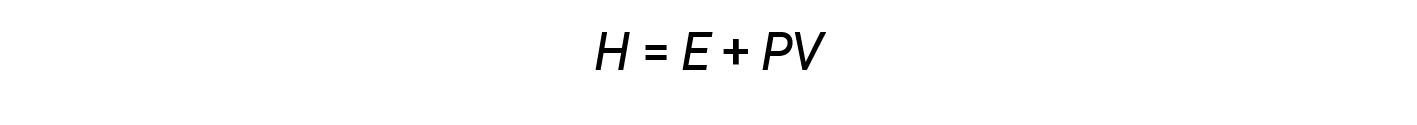
焓是一种状态函数。特定物质的焓值不能直接测量；只能确定化学或物理过程的焓变。对于在恒定压力（许多化学和物理变化的常见条件）下发生的过程，焓变（Δ H ）为：

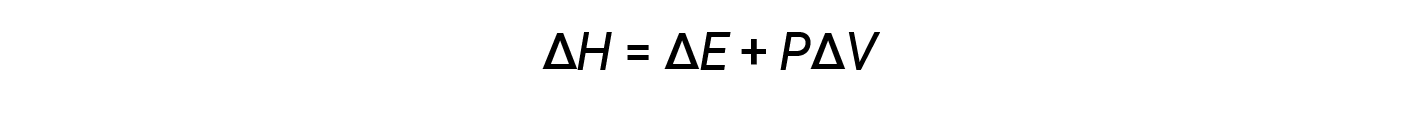
数学乘积 P Δ V 表示功（ w ），即膨胀或压力-体积功。按照它们的定义，＆lt; V 和w的算术符号将始终相反：

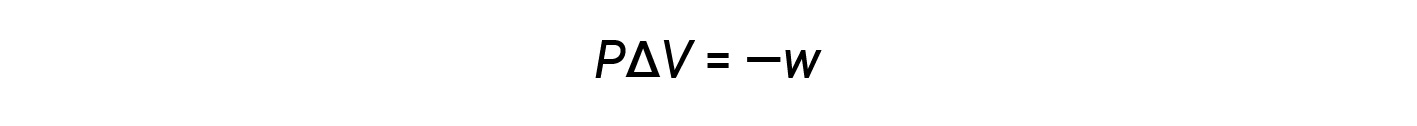
代入该方程式和恒定压力下内能的定义（Δ E = q _p + w ）到焓变方程中得出：

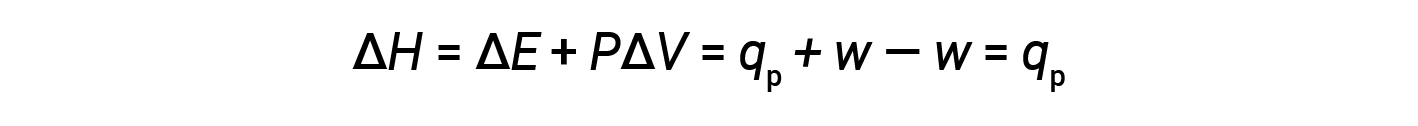
其中 q _p 是在恒定压力下的反应热。

因此，如果化学或物理过程是在恒定压力下进行的，而唯一的功是由膨胀或收缩引起的（ PV 功），则热流（ q _p ）和该过程的焓变（Δ H ）相等。

运行本生灯时散发的热量等于发生的甲烷燃烧反应的焓变，因为它发生在基本恒定的大气压下。化学家通常在正常大气条件下，恒定外压和 q _p =＆Delta; H 的条件下进行实验，这使焓成为最方便的选择确定化学反应的热变化。

焓变的负值＆lt; H ＆lt; 0表示放热反应（热量散发到周围环境）；正值＆lt; H ＆gt; 0表示吸热反应（从周围环境吸收的热量）。如果化学方程式的方向相反，则其 H 的算术符号会更改（在一个方向上吸热的过程在相反方向上放热）。

从概念上讲，Δ E （热量和功的度量）和Δ H （恒定压力下的热量的度量）都表示状态函数的变化对于系统。在体积变化的过程中，Δ V 小（冰融化），而Δ E 和Δ H 相同。但是，如果体积变化很大（水蒸发），则作为功率传递的能量将很大。因此，＆lt; E 和＆Delta; H 的值明显不同。

本文改编自 Openstax，化学2e，第5.3节：焓。