9.5:
Trends in Lattice Energy: Ion Size and Charge
Lattice energy is associated with the formation or separation of an ionic lattice. Yet, when sodium chloride or magnesium oxide form, their lattice energy differs significantly. Why does each ionic compound have a different lattice energy, and which factors does it depend on?
An ionic compound consists of an orderly arrangement of a large number of charged ions attracted to each other by electrostatic interactions.
According to Coulomb’s law, the potential energy of two ions is inversely proportional to the distance between the ions, which in turn depends on the ionic radius.
In the periodic table, the ionic radius of the alkali and alkaline earth metals increases down the column. As the size of the metal ion increases, the distance between ions, or the bond length, becomes larger as well. For example, the bond length of lithium bromide and potassium bromide differs between 217 pm and 282 pm, respectively.
Due to the increased internuclear distance, the attraction between the ions decreases and it becomes much easier to separate the ions. Thus the lattice energy to separate solid lithium bromide is larger than for potassium bromide being +807 kJ/mol versus +682 kJ/mol, respectively.
In addition to the ionic radius, the magnitude of lattice energy also depends on the ion charges. According to Coulomb’s law, the potential energy of ions is directly proportional to the product of their charges.
Consider two ionic compounds sodium fluoride and calcium oxide. The ionic distance in both compounds is similar, but the lattice energy of calcium oxide is almost four times greater than sodium fluoride.
Both sodium and fluoride are monovalent ions; the product of their charge is 1. However, calcium and oxide ions are divalent and the product of their charge is 4, which is four times greater than sodium fluoride.
This is why it takes nearly four times as much energy to separate the calcium oxide into gaseous ions as compared to sodium fluoride.
Thus, the magnitude of lattice energy is directly proportional to the product of the ion charges and is inversely proportional to the distance between the ions.
9.5:
Trends in Lattice Energy: Ion Size and Charge
An ionic compound is stable because of the electrostatic attraction between its positive and negative ions. The lattice energy of a compound is a measure of the strength of this attraction. The lattice energy (ΔHlattice) of an ionic compound is defined as the energy required to separate one mole of the solid into its component gaseous ions. For the ionic solid sodium chloride, the lattice energy is the enthalpy change of the process:
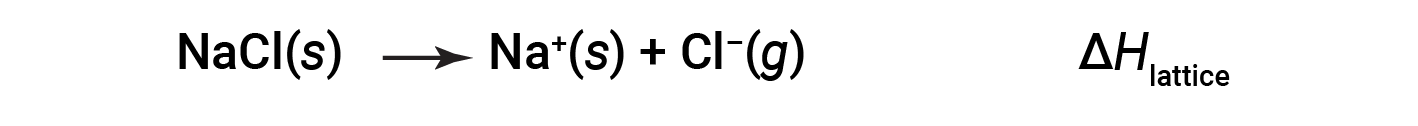
Conventions
Here, the convention is used where the ionic solid is separated into ions, meaning the lattice energies will be endothermic (positive values). Another way is to use an equivalent but opposite convention, wherein the lattice energy is exothermic (negative values) and described as the energy released when ions combine to form a lattice. Thus, make sure to confirm which definition is used when looking up lattice energies in another reference. In both cases, a larger magnitude for lattice energy indicates a more stable ionic compound. For sodium chloride, ΔHlattice = 769 kJ. Thus, it requires 769 kJ to separate one mole of solid NaCl into gaseous Na+ and Cl– ions. When one mole each of gaseous Na+ and Cl– ions form solid NaCl, 769 kJ of heat is released.
Coulomb’s Law and Lattice Energy
The lattice energy ΔHlattice of an ionic crystal can be expressed by the following equation (derived from Coulomb’s law, governing the forces between electric charges):
ΔHlattice = C(Z +)(Z−)/Ro
in which C is a constant that depends on the type of crystal structure; Z+ and Z– are the charges on the ions, and Ro is the interionic distance (the sum of the radii of the positive and negative ions). Thus, the lattice energy of an ionic crystal increases rapidly as the charges of the ions increase and the sizes of the ions decrease. When all other parameters are kept constant, doubling the charge of both the cation and anion quadruples the lattice energy.
Examples
- The lattice energy of LiF (Z+ and Z– = 1) is 1023 kJ/mol, whereas that of MgO (Z+ and Z– = 2) is 3900 kJ/mol (Ro is nearly the same — about 200 pm for both compounds).
- Different interatomic distances produce different lattice energies. For example, compare the lattice energy of MgF2 (2957 kJ/mol) to that of MgI2 (2327 kJ/mol) to observe the effect on lattice energy of the smaller ionic size of F– as compared to I–.
- The precious gem ruby is aluminum oxide, Al2O3, containing traces of Cr3+. The compound Al2Se3 is used in the fabrication of some semiconductor devices. In these two ionic compounds, the charges Z+ and Z– are the same, so the difference in lattice energy depends upon Ro. Since the O2– ion is smaller than the Se2– ion, the Al2O3 has a shorter interionic distance than Al2Se3 and has, therefore, larger lattice energy.
- Another example is zinc oxide, ZnO, compared to NaCl. ZnO has a larger lattice energy because the Z values of both the cation and the anion in ZnO are greater, and the interionic distance of ZnO is smaller than that of NaCl.
This text is adapted from Openstax, Chemistry 2e, Section 7.5: Strengths of Ionic and Covalent Bonds.
