9.5: Tendências em Energia Reticular: Tamanho e Carga de Iões
Um composto iónico é estável devido à atração eletrostática entre os seus iões positivos e negativos. A energia reticular de um composto é uma medida da força desta atração. A energia reticular (ΔHreticular) de um composto iónico é definida como a energia necessária para separar um mole do sólido nos seus iões gasosos constituintes. Para o sólido iónico cloreto de sódio, a energia reticular é a alteração da entalpia do processo:
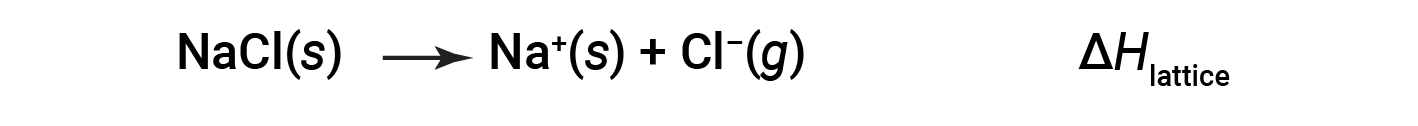
Convenções
Aqui, é usada a convenção onde o sólido iónico é separado em iões, o que significa que as energias reticulares serão endotérmicas (valores positivos). Outra forma é usar uma convenção equivalente, mas oposta, na qual a energia reticular é exotérmica (valores negativos) e descrita como a energia libertada quando os iões se combinam para formar uma rede. Assim, certifique-se de confirmar que definição é usada ao procurar energias reticulares em outra referência. Em ambos os casos, uma magnitude maior para a energia reticular indica um composto iónico mais estável. Para cloreto de sódio, ΔHreticular = 769 kJ. Portanto, requer 769 kJ para separar um mole de NaCl sólido nos iões gasosos Na+ e Cl–. Quando um mole de cada um dos iões gasosos Na+ e Cl– formam NaCl sólido, são libertados 769 kJ de calor.
A Lei de Coulomb e a Energia Reticular
A energia reticular ΔHreticular de um cristal iónico pode ser expressa pela seguinte equação (derivada da lei de Coulomb, que rege as forças entre cargas elétricas):
ΔHreticular = C(Z +)(Z−)/Ro
em que C é uma constante que depende do tipo de estrutura cristalina; Z+ e Z– são as cargas dos iões, e Ro é a distância interiónica (a soma dos raios dos iões positivos e negativos). Assim, a energia reticular de um cristal iónico aumenta rapidamente à medida que as cargas dos iões aumentam e os tamanhos dos iões diminuem. Quando todos os outros parâmetros são mantidos constantes, a duplicação da carga tanto do catião como do anião quadruplica a energia reticular.
Exemplos
- A energia reticular de LiF (Z+ e Z– = 1) é de 1023 kJ/mol, enquanto que a de MgO (Z+ e Z– = 2) é de 3900 kJ/mol (Ro é quase igual — cerca de 200 pm para ambos os compostos).
- Diferentes distâncias interatómicas produzem diferentes energias reticulares. Por exemplo, compare a energia reticular de MgF2 (2957 kJ/mol) com a de MgI2 (2327 kJ/mol) para observar o efeito na energia reticular do tamanho iónico menor de F– em comparação com I–.
- A jóia preciosa rubi é óxido de alumínio, Al2O3, contendo vestígios de Cr3+. O composto Al2Se3 é usado na fabricação de alguns dispositivos semicondutores. Nestes dois compostos iónicos, as cargas Z+ e Z– são as mesmas, de modo que a diferença na energia reticular depende de Ro. Como o ião O2– é menor que o ião Se2–, Al2O3 tem uma distância interiónica menor que Al2Se3 e tem, portanto, maior energia reticular.
- Outro exemplo é o óxido de zinco, ZnO, comparado com NaCl. ZnO tem uma maior energia reticular porque os valores de Z do catião e do anião no ZnO são maiores, e a distância interiónica de ZnO é menor que a do NaCl.
Este texto é adaptado de Openstax, Chemistry 2e, Section 7.5: Strengths of Ionic and Covalent Bonds.


