Overview
Source: Laboratory of Dr. Michael Evans — Georgia Institute of Technology
The equilibrium constant, K, for a chemical system is the ratio of product concentrations to reactant concentrations at equilibrium, each raised to the power of their respective stoichiometric coefficients. Measurement of K involves determination of these concentrations for systems in chemical equilibrium.
Reaction systems containing a single colored component can be studied spectrophotometrically. The relation between absorbance and concentration for the colored component is measured and used to determine its concentration in the reaction system of interest. Concentrations of the colorless components can be calculated indirectly using the balanced chemical equation and the measured concentration of the colored component.
In this video, the Beer's law curve for Fe(SCN)2+ is determined empirically and applied to the measurement of K for the following reaction:
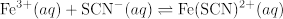
Four reaction systems with different initial concentrations of reactants are investigated to illustrate that K remains constant irrespective of initial concentrations.
Principles
Every chemical reaction is associated with an equilibrium constant K, which reflects the ratio of product concentrations to reactant concentrations at chemical equilibrium. For the generic reaction a A + b B  c C + d D, the equilibrium constant is defined as
c C + d D, the equilibrium constant is defined as

where the concentrations on the right-hand side of the equation are molarities at equilibrium. This equation is known as the equilibrium expression for the reaction. In chemical systems that are not in equilibrium, the forward and reverse reactions occur at different rates until the concentrations of reactants and products satisfy the equilibrium expression.
To measure the value of K for a system in chemical equilibrium, it is necessary to determine the concentrations of reactants and products either directly or indirectly. Spectrophotometric methods for the determination of K involve direct measurement of the concentration of one colored component and indirect measurement of the others. Visible spectroscopy of the colored component at known concentrations reveals the relation between absorbance and concentration for this component. According to Beer's law, this relation has the form

where e is the molar absorptivity of the component in L/mol-cm, l is the path length of light through the sample in cm, c is the molarity of the component in mol/L, and A is the absorbance.
The Beer's law curve for the colored component can be applied to a reaction system in equilibrium to determine the concentration of this component from absorbance measurements (Figure 1). Concentrations of the remaining reactants and products can then be calculated by adjusting initial concentrations based on the measured molarity of the colored species.
The system studied here is the reaction of iron (III) cation with thiocyanate anion to form an iron (III) thiocyanate complex.

The equilibrium expression for this reaction system is

where the eq subscript denotes equilibrium concentrations. The iron (III) thiocyanate product is orange, but both reactants are colorless in aqueous solution. Hence, [Fe(SCN)2+]eq can be determined directly from absorbance measurements.

Equilibrium concentrations of the reactants can be calculated by subtracting the equilibrium concentration of the product from the initial concentrations of the reactants. An Initial-Change-Equilibrium (ICE) table illustrates how initial and equilibrium concentrations are related (Table 1).

Repeated trials of this experiment involving different initial concentrations of reactants should yield the same value of K, as the value of K is independent of concentration.

Figure 1. Beer's law curve for iron (III) thiocyanate.
| Fe3+ | SCN– | Fe(SCN)2+ | |
| Initial | [Fe3+]i | [SCN–]i | 0 |
| Change | –[Fe(SCN)2+]eq | –[Fe(SCN)2+]eq | +[Fe(SCN)2+]eq |
| Equilibrium | [Fe3+]i – [Fe(SCN)2+]eq | [SCN–]i – [Fe(SCN)2+]eq | [Fe(SCN)2+]eq |
Table 1. An Initial-Change-Equilibrium (ICE) table that illustrates how initial and equilibrium concentrations are related.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Determining the Beer's Law Curve for Fe(SCN)2+
- Calibrate a visible spectrophotometer using distilled water as a blank.
- Add 1.0 mL of 1.0 × 10-4 M Fe(NO3)3 solution to a test tube.
- To the same test tube, add 5.0 mL of 0.50 M KSCN solution.
- To the same test tube, add 4.0 mL of 0.10 M HNO3 solution. Cover the tube with a gloved finger and gently shake to mix.
- Use a Pasteur pipette to transfer a small quantity of the solution to a cuvette. Ensure that the liquid level is above the path of the light beam in the spectrophotometer.
- Place the cuvette in the spectrophotometer, so the light passes through the transparent sides.
- Acquire a spectrum and record the λmax value and the absorbance at λmax.
- In order to construct a Beer's law curve, additional solutions with known concentrations of Fe(SCN)2+ must be prepared and measured. Repeat steps 2 – 7 using the volumes of Fe(NO3)3, KSCN, and HNO3 solutions in Table 2. Make sure to use the same cuvette for all measurements, rinsing 3 times with distilled water in between each sample.
- Plot the measured absorbance versus the concentrations of Fe(SCN)2+ in each test tube and determine the line of best fit for the data. The slope of this line is the molar absorptivity and the path length is 1 cm.
2. Measuring K for the Iron (III) Thiocyanate System
- Prepare 4 medium test tubes containing the indicated volumes of 0.0025 M Fe(NO3)3, 0.0025 M KSCN, and 0.10 M HNO3 solutions in Table 3.
- Cover each tube with a finger and gently shake to mix. Allow them to stand for at least 10 min. This resting period ensures that the solutions are at chemical equilibrium.
- Use a Pasteur pipette to transfer a small quantity of solution 6 to a cuvette. Ensure that the liquid level is above the path of the light beam in the spectrophotometer.
- Acquire a spectrum and record the absorbance at λmax.
- Multiple reactions with different initial concentrations of reactants can be studied to illustrate that K does not depend on concentration. To determine K for different initial conditions, repeat steps 3 and 4 for solutions 7 – 9.
| Tube Number | Volume 1.0 x 10–4 M Fe(NO3)3 (mL) |
Volume 0.50 M KSCN (mL) |
Volume 0.10 M HNO3 (mL) |
| 1 | 1.0 | 5.0 | 4.0 |
| 2 | 2.0 | 5.0 | 3.0 |
| 3 | 3.0 | 5.0 | 2.0 |
| 4 | 4.0 | 5.0 | 1.0 |
| 5 | 5.0 | 5.0 | 0.0 |
Table 2. Appropriate volumes of Fe(NO3)3, KSCN, and HNO3 solutions to be placed in tubes 2 - 5.
| Tube Number | Volume 0.0025 M Fe(NO3)3 (mL) |
Volume 0.0025 M KSCN (mL) |
Volume 0.10 M HNO3 (mL) |
| 6 | 1.0 | 1.0 | 5.0 |
| 7 | 1.0 | 2.0 | 4.0 |
| 8 | 2.0 | 2.0 | 3.0 |
| 9 | 2.0 | 3.0 | 2.0 |
Table 3. Appropriate volumes of 0.0025 M Fe(NO3)3, 0.0025 M KSCN, and 0.10 M HNO3 solutions.
Determining the equilibrium constant of a chemical reaction can provide important information about the extent to which it will form products over time.
Every chemical reaction is associated with an equilibrium constant, K, which reflects the ratio of the concentrations of the products and reactants when the reaction has stopped progressing. To measure K, these concentrations must be determined.
If a reaction contains a single colored component, its interaction with light can be measured to discern its concentration. The concentrations of the uncolored components can then be calculated indirectly using the balanced chemical equation. This video will illustrate the use of a spectrophotometer to empirically determine the equilibrium constant for an iron thiocyanante reaction.
Most chemical reactions proceed in both forward and reverse directions. As the reaction progresses, it reaches a point where the forward and reverse reactions occur at the same rate. This is known as chemical equilibrium. At this steady state, the ratio of product concentrations to reactant concentrations, each raised to the power of their stoichiometric coefficients, corresponds to the equilibrium constant, K. To measure K for a system of interest, the coefficients should be known, and the concentrations must be determined, either directly or indirectly. According to the Beer-Lambert law, the concentration of a colored species is proportional to its absorbance, which is the amount of energy it absorbs at a specific wavelength of light. This can be expressed mathematically, where A is absorbance, epsilon is the molar attenuation coefficient, which is compound-specific, l is the path length through the sample, and c is concentration. A calibration curve is created by testing multiple solutions of known concentration, and plotting the resulting absorbance values. With this calibration curve, solutions of unknown concentration can be studied. Absorbance measurements are used to determine the concentration of the colored species. Then, the concentrations of the remaining reactants and products can be calculated. The following procedure will study the reaction of iron three with thiocyanate to form an iron thiocyanate complex.
Once the concentrations have been determined, the value for K can be calculated with an Initial-Change-Equilibrium, or ICE, table which will be explained further in the results.
Now that you understand how spectrophotometric methods can be used to determine the equilibrium constant, you are ready to begin the procedure.
Before measuring the sample, a calibration curve must be generated.
To begin, zero a UV-vis spectrophotometer using distilled water as a blank to represent no absorbance. When inserting a cuvette into the spectrophotometer, ensure that it is oriented so light passes through the transparent sides, and that the liquid level is above the path of the beam.
Then, prepare 5 test tubes containing the indicated volumes of each reactant solution as shown in the text protocol, which will yield varying concentrations of the product. Cover each tube with a gloved finger, and gently shake to mix. Allow the tubes to rest for 10 min.
Use a Pasteur pipette to transfer a small quantity of the mid-concentration sample, solution 3, to a cuvette, and place it in the spectrophotometer. Acquire a spectrum and record the λmax (maximum wavelength), lambda max, and its absorbance. Then, beginning with the most dilute solution, measure the absorbance of all remaining solutions at the λmax (lambda max). Use the same cuvette for all measurements, making sure to rinse 3 times in between each sample. Repeat this process for solutions 2 – 5.
Plot the measured absorbance versus concentration of iron thiocyanate for each solution. Determine the line of best fit for the data. The slope of this line is the molar attenuation coefficient.
Now that the data for the standard solutions has been acquired, prepare four medium test tubes containing the indicated volumes of solutions as shown in the text protocol.
Cover each tube with a finger and gently shake to mix. Allow them to stand for at least 10 min. This resting period allows the solutions to reach chemical equilibrium.
Use a Pasteur pipette to transfer a small quantity of solution 6 to the cuvette, and place it in the spectrophotometer. Acquire a spectrum and record the absorbance measured at the predetermined λmax. Repeat this process for solutions 7 through 9.
Once all of the samples have been measured, the molarity and absorbance data for solutions 1 – 5 can be analyzed. A large excess of thiocyanate was used to ensure that all of the iron reacted, which simplifies the analysis.
The data is plotted to create a calibration curve. The path length of light, l, is typically 1 cm, and can be factored out of the calculations. The slope of the line, which was calculated to be 7600, is therefore the attenuation coefficient. For the test solutions 6 – 9, this value and the absorbance are used to calculate the iron thiocyanate concentrations at equilibrium. With this data, the ICE table could then be utilized.
The initial reactant concentrations are based on the known molarities of iron and thiocyanate added to the solution, and the total volume of the reaction. Because the product is formed from the 1:1 reaction of iron and thiocyanate, the equilibrium concentration of each decreases by the amount of product formed. The equilibrium concentration of each species is now known. These values are used to calculate the equilibrium constant for each solution. The values are roughly constant over the range of concentrations studied.
The concept of the equilibrium constant is important to a wide range of scientific fields. The equilibrium constant can be used to provide useful information about the extent to which a reaction will form products over time. In this example, two reactions containing crystal violet were observed.
The first solution was composed of crystal violet and sodium hydroxide. The color was observed to rapidly change from purple to colorless. This reaction has a very large K value, indicating that the products form nearly completely over time.
Crystal violet was then reacted with sodium acetate. This solution remained purple indefinitely. This reaction has a very low K value, so it does not proceed forward to a significant degree.
Finally, the dissociation constant — a specific type of equilibrium constant — can be used to describe protein behavior. In this example, changes in the structure of RNA were monitored in magnesium reaction buffers.
Purified RNA was mixed into solution with known concentrations of magnesium, and allowed to reach equilibrium. Then, the resulting RNA structure was plotted.
In this case, higher concentrations of magnesium caused reactive sites on RNA to be less protected, producing a Kd that was half the value.
You've just watched JoVE's introduction to spectrophotometric determination of the equilibrium constant. You should now understand the relationship defined by the Beer-Lambert law, how to determine concentration from absorbance using a spectrophotometer, and how to calculate an equilibrium constant using equilibrium concentrations.
Thanks for watching!
Subscription Required. Please recommend JoVE to your librarian.
Results
Table 4 lists the absorbance and concentration data for solutions 1 – 5. Concentrations of Fe(SCN)2+ were determined from initial concentrations of Fe3+ under the assumption that all of the Fe3+ is converted to Fe(SCN)2+. A large excess of SCN- was used in tubes 1 – 5 to ensure that this assumption holds true.
The molarity [Fe(SCN)2+] and absorbance are plotted in Figure 2. The measured absorbances agree well with Beer's law.
Table 5 lists measured absorbances and calculated K values for tubes 6 – 9. K values were determined using the ICE table method. Initial reactant concentrations were based on the known molarities of Fe3+ and SCN- in the reactant solutions and the total volume of the reaction (10 mL). The equilibrium concentration of Fe(SCN)2+ was determined by dividing measured absorbance by the molar absorptivity of Fe(SCN)2+. Because all of the product was formed from the 1:1 reaction of Fe3+ and SCN-, the equilibrium concentration of Fe(SCN)2+ corresponds to the decrease in concentration of the reactants. Table 6 shows the process for test tube 6.
The equilibrium constant is calculated from the concentrations in the equilibrium row. For test tube 6,

The mean K value was 147 ± 11, illustrating that K is roughly constant over the range of concentrations studied.

Figure 2. Line graph of Absorbance versus Concentration for Fe(SCN)2+.
| Tube | [Fe(SCN)2+] (mol/L) | Absorbance |
| 1 | 1.00 x 10–5 | 0.10 |
| 2 | 2.00 x 10–5 | 0.20 |
| 3 | 3.00 x 10–5 | 0.25 |
| 4 | 4.00 x 10–5 | 0.32 |
| 5 | 5.00 x 10–5 | 0.42 |
Table 4. Absorbance versus Concentration Data for Fe(SCN)2+.
| Tube | Absorbance | K |
| 6 | 0.120 | 136 |
| 7 | 0.268 | 161 |
| 8 | 0.461 | 142 |
| 9 | 0.695 | 150 |
Table 5. Measured absorbance values and calculated K for the reaction of iron (III) with thiocyanate.
| [Fe3+] (mol/L) | [SCN–] (mol/L) | [Fe(SCN)2+] (mol/L) | |
| Initial | 3.57 x 10–4 | 3.57 x 10–4 | 0 |
| Change | –1.58 x 10–5 | –1.58 x 10–5 | +1.58 x 10–5 |
| Equilibrium | 3.41 x 10–4 | 3.41 x 10–4 | 1.58 x 10–5 |
Table 6. The ICE table that illustrates the process used for test tube 6.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
The equilibrium constant provides useful information about the extent to which a reaction will proceed to form products over time. Reactions with a large value of K, much larger than 1, will form products nearly complete given enough time (Figure 3). Reactions with a value of K less than 1 will not proceed forward to a significant degree. The equilibrium constant thus serves as a measure of the feasibility of a chemical reaction.

Figure 3. The equilibrium constant of this reaction is greater than 1. A significant amount of colored product forms in each case, even though the initial concentrations of reactants differ.
The equilibrium constant also provides useful thermodynamic information about the changes in free energy, enthalpy, and entropy in the course of a chemical reaction. The equilibrium constant is related to the free energy change of reaction:

The free energy change of reaction is in turn related to the enthalpy and entropy changes of reaction:

Measurements of the temperature dependence of K can reveal the enthalpy change ΔH and the entropy change ΔS for a reaction. In addition to providing chemists with insight into patterns in molecular behavior, tables of thermodynamic data can be used to identify reactions with favorable thermodynamic properties. For example, redox reactions that release large amounts of energy (associated with negative ΔG values) are attractive candidates for batteries.
Values of K for acid dissociation reactions (Ka values) are useful for predicting the outcomes of acid-base reactions, which are thermodynamically controlled. Strong acids are associated with large Ka values and weak acids with small Ka values. pH indicators are weak acids with differently colored acidic and basic forms, and the pKa (the negative base-10 logarithm of Ka) of an indicator represents the pH at which a color change occurs as an acid or base is added to a solution of the indicator.
Similarly, Ka values are used in the preparation of buffer solutions to achieve a target pH value. The pKa of a weak acid represents the pH at which the acid and its conjugate base are present in the solution in equal concentrations. When equal amounts of a weak acid and its conjugate base are dissolved in a solution, the pH of the solution equals the pKa of the weak acid.
Subscription Required. Please recommend JoVE to your librarian.




