Overview
מקור: המעבדה של ד"ר מייקל אוונס — המכון הטכנולוגי של ג'ורג'יה
קבוע שיווי המשקל, K, עבור מערכת כימית הוא היחס בין ריכוזי המוצר לריכוזים מגיבים בשיווי משקל, כל אחד מהם הועלה לעוצמה של מקדמי הסטויצ'יומטריים שלהם. מדידת K כרוכה בקביעת ריכוזים אלה עבור מערכות בשיווי משקל כימי.
ניתן לחקור מערכות תגובה המכילות רכיב צבעוני יחיד באופן ספקטרופוטומטרי. הקשר בין ספיגה לריכוז עבור הרכיב הצבעוני נמדד ומשמש לקביעת ריכוזו במערכת התגובה של העניין. ריכוזים של הרכיבים חסרי הצבע ניתן לחשב בעקיפין באמצעות המשוואה הכימית המאוזנת ואת הריכוז הנמדד של הרכיב הצבעוני.
בסרטון זה, עקומת חוק הבירה עבור Fe(SCN)2+ נקבעת אמפירית ומוחלת על מדידת K לתגובה הבאה:
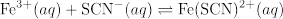
ארבע מערכות תגובה עם ריכוזים ראשוניים שונים של מגיבים נחקרות כדי להמחיש כי K נשאר קבוע ללא קשר לריכוזים הראשוניים.
Principles
כל תגובה כימית קשורה עם שיווי משקל קבוע K, אשר משקף את היחס בין ריכוזי המוצר לריכוזים מגיבים בשיווי משקל כימי. עבור התגובה הכללית A + b B 
C C + d D, קבוע שיווי המשקל מוגדר כ
שבו הריכוזים בצד ימין של המשוואה הם טחנות בשיווי משקל. משוואה זו ידועה כביטוי שיווי המשקל לתגובה. במערכות כימיות שאינן בשיווי משקל, התגובות קדימה ואחורה מתרחשות בקצבים שונים עד שריכוזים של מגיבים ומוצרים מספקים את ביטוי שיווי המשקל.
כדי למדוד את הערך של K עבור מערכת בשיווי משקל כימי, יש צורך לקבוע את הריכוזים של מגיבים ומוצרים במישרין או בעקיפין. שיטות ספקטרופוטומטריות לקביעת K כרוכות במדידה ישירה של הריכוז של רכיב צבעוני אחד ומדידה עקיפה של האחרים. ספקטרוסקופיה גלויה של הרכיב הצבעוני בריכוזים ידועים מגלה את הקשר בין ספיגה לריכוז עבור רכיב זה. על פי החוק של באר, לקשר זה יש את הטופס
כאשר e הוא ספיגת הטוחנת של הרכיב ב L / מול-ס"מ, l הוא אורך הנתיב של אור דרך המדגם בס"מ, c הוא הטוחנת של הרכיב מול / L, ו- A הוא הספיגה.
ניתן להחיל את עקומת החוק של הבירה על הרכיב הצבעוני על מערכת תגובה בשיווי משקל כדי לקבוע את ריכוז הרכיב הזה ממדידות ספיגה (איור 1). לאחר מכן ניתן לחשב את הריכוזים של המגיבים והמוצרים הנותרים על ידי התאמת הריכוזים הראשוניים בהתבסס על הטוחנת הנמדדת של המינים הצבעוניים.
המערכת שנחקרה כאן היא התגובה של cation ברזל (III) עם אניון תיוצינאט כדי ליצור קומפלקס תיוצינאט ברזל (III).
ביטוי שיווי המשקל עבור מערכת תגובה זו הוא
כאשר הכתב התת-קרקעי eq מציין ריכוזי שיווי משקל. המוצר תיוציאנט ברזל (III) הוא כתום, אבל שני המגיבים הם חסרי צבע פתרון מימי. לפיכך, [Fe(SCN)2+]eq ניתן לקבוע ישירות ממדידות ספיגה.
ריכוזי שיווי משקל של המגיבים ניתן לחשב על ידי חיסור ריכוז שיווי המשקל של המוצר מהריכוזים הראשוניים של המגיבים. טבלה ראשונית-שינוי-שיווי משקל (ICE) ממחישה כיצד ריכוזי ראשוניים ושיווי משקל קשורים(טבלה 1).
ניסויים חוזרים ונשנים של ניסוי זה הכולל ריכוזים ראשוניים שונים של מגיבים צריכים להניב את אותו ערך של K, שכן הערך של K אינו תלוי בריכוז.
איור 1. עקומת חוק הבירה עבור ברזל (III) תיוציאנט.
| Fe3+ | SCN– | Fe (SCN)2+ | |
| הראשונית | [Fe3+] i | [SCN–] i | 0 |
| שינוי | –[Fe(SCN)2+]eq | –[Fe(SCN)2+]eq | +[Fe(SCN)2+]eq |
| שיווי משקל | [Fe3+] i – [Fe(SCN)2+]eq | [SCN–] i – [Fe(SCN)2+]eq | [Fe(SCN)2+] eq |
טבלה 1. טבלת שיווי משקל ראשוני-שינוי(ICE) הממחישה כיצד ריכוזי ראשוניים ושיווי משקל קשורים.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. קביעת עקומת חוק הבירה ל-Fe(SCN)2+
- כייל ספקטרופוטומטר גלוי באמצעות מים מזוקקים כריקים.
- הוסף 1.0 מ"ל של 1.0 × 10-4 M Fe(NO3)3 פתרון מבחנה.
- לאותה מבחנה, הוסף 5.0 מ"ל של פתרון KSCN 0.50 M.
- לאותה מבחנה, להוסיף 4.0 מ"ל של פתרון 0.10 M HNO3. מכסים את הצינור באצבע עם כפפות ומנערים בעדינות כדי לערבב.
- השתמש פיפטה פסטר להעביר כמות קטנה של הפתרון cuvette. ודא כי רמת הנוזל היא מעל הנתיב של קרן האור בספקטרופוטומטר.
- מניחים את הקובט בספקטרופוטומטר, כך שהאור עובר דרך הצדדים השקופים.
- רכש ספקטרום ורשום את הערךהמרבי של λ ואת הספיגה ב- λmax.
- על מנת לבנות עקומת חוק בירה, יש להכין ולמדוד פתרונות נוספים עם ריכוזים ידועים של Fe(SCN)2+. חזור על שלבים 2 – 7 באמצעות אמצעי האחסון של פתרונות Fe(NO3)3, KSCN ו- HNO3 בטבלה 2. הקפד להשתמש באותה cuvette עבור כל המדידות, שטיפה 3 פעמים עם מים מזוקקים בין כל מדגם.
- התווה את הספיגה הנמדדת לעומת הריכוזים של Fe(SCN)2+ בכל מבחנה ולקבוע את קו ההתאמה הטובה ביותר לנתונים. השיפוע של קו זה הוא ספיגת הטוחנת ואורך השביל הוא 1 ס"מ.
2. מדידת K למערכת הברזל (III) תיוצינאט
- הכן 4 מבחנות בינוניות המכילות את הנפחים המצוינים של 0.0025 M Fe(NO3)3, 0.0025 M KSCN ו- 0.10 M HNO3 פתרונות בטבלה 3.
- מכסים כל שפופרת באצבע ומנערים בעדינות כדי לערבב. אפשר להם לעמוד לפחות 10 דקות. תקופת מנוחה זו מבטיחה כי הפתרונות נמצאים בשיווי משקל כימי.
- השתמש פיפטה פסטר להעביר כמות קטנה של פתרון 6 ל cuvette. ודא כי רמת הנוזל היא מעל הנתיב של קרן האור בספקטרופוטומטר.
- לרכוש ספקטרום ולתעד את הספיגה ב λמקסימום.
- תגובות מרובות עם ריכוזים ראשוניים שונים של מגיבים ניתן ללמוד כדי להמחיש כי K אינו תלוי בריכוז. כדי לקבוע K עבור תנאים התחלתיים שונים, חזור על שלבים 3 ו- 4 עבור פתרונות 7 – 9.
| מספר צינור | נפח 1.0 x 10–4 M Fe(NO3)3 (מ"ל) |
נפח 0.50 M KSCN (מ"ל) |
נפח 0.10 מ' HNO3 (מ"ל) |
| 1 | 1.0 | 5.0 | 4.0 |
| 2 | 2.0 | 5.0 | 3.0 |
| 3 | 3.0 | 5.0 | 2.0 |
| 4 | 4.0 | 5.0 | 1.0 |
| 5 | 5.0 | 5.0 | 0.0 |
טבלה 2. נפחים מתאימים של Fe(NO3)3, KSCN ו- HNO3 פתרונות שיוצבו בצינורות 2 - 5.
| מספר צינור | נפח 0.0025 M Fe(NO3)3 (מ"ל) |
נפח 0.0025 M KSCN (מ"ל) |
נפח 0.10 מ' HNO3 (מ"ל) |
| 6 | 1.0 | 1.0 | 5.0 |
| 7 | 1.0 | 2.0 | 4.0 |
| 8 | 2.0 | 2.0 | 3.0 |
| 9 | 2.0 | 3.0 | 2.0 |
טבלה 3. נפחים מתאימים של 0.0025 M Fe(NO3)3, 0.0025 M KSCN ופתרונות HNO3 של 0.10 M.
קביעת קבוע שיווי המשקל של תגובה כימית יכולה לספק מידע חשוב על המידה שבה היא תיצור מוצרים לאורך זמן.
כל תגובה כימית קשורה קבוע שיווי משקל, K, אשר משקף את היחס של הריכוזים של המוצרים והמגיבים כאשר התגובה הפסיקה להתקדם. כדי למדוד K, ריכוזים אלה חייבים להיקבע.
אם תגובה מכילה רכיב צבעוני אחד, ניתן למדוד את האינטראקציה שלה עם האור כדי להבחין בריכוז שלה. לאחר מכן ניתן לחשב את הריכוזים של הרכיבים הלא צבעוניים בעקיפין באמצעות המשוואה הכימית המאוזנת. וידאו זה ימחיש את השימוש בספקטרופוטומטר כדי לקבוע אמפירית את קבוע שיווי המשקל לתגובה תיוציאנטה מברזל.
רוב התגובות הכימיות ממשיכות הן בכיוונים קדימה והן בכיוונים הפוכים. ככל שהתגובה מתקדמת, היא מגיעה לנקודה שבה התגובות קדימה ואחורה מתרחשות באותו קצב. זה ידוע כשווי משקל כימי. במצב יציב זה, היחס בין ריכוזי המוצר לריכוזים מגיבים, שכל אחד מהם עלה לעוצמה של מקדמי הסטויצ'יומטריים שלהם, מתאים קבוע שיווי המשקל, K. כדי למדוד K עבור מערכת עניין, המקדחים צריכים להיות ידועים, ואת הריכוזים חייב להיקבע, במישרין או בעקיפין. על פי חוק באר-למברט, ריכוז המינים הצבעוניים פרופורציונלי לספיגתו, שהיא כמות האנרגיה שהוא סופג באורך גל מסוים של אור. זה יכול לבוא לידי ביטוי מתמטית, כאשר A הוא ספיגה, אפסילון הוא מקדם ההנחיה הטוחנת, שהוא ספציפי לתרכובת, l הוא אורך הנתיב דרך המדגם, ו- c הוא ריכוז. עקומת כיול נוצרת על-ידי בדיקת פתרונות מרובים של ריכוז ידוע, והתוויית ערכי הספיגה המתקבלים. עם עקומת כיול זו, ניתן ללמוד פתרונות של ריכוז לא ידוע. מדידות ספיגה משמשות לקביעת הריכוז של המינים הצבעוניים. לאחר מכן, ניתן לחשב את הריכוזים של המגיבים והמוצרים הנותרים. ההליך הבא ילמד את התגובה של ברזל שלוש עם תיוציאנט כדי ליצור קומפלקס תיוציאנט ברזל.
לאחר הריכוזים נקבעו, הערך עבור K ניתן לחשב עם ראשוני-שינוי-שיווי משקל, או ICE, טבלה אשר יוסבר עוד יותר בתוצאות.
עכשיו שאתה מבין איך ניתן להשתמש בשיטות ספקטרופוטומטריות כדי לקבוע את קבוע שיווי המשקל, אתה מוכן להתחיל את ההליך.
לפני מדידת המדגם, יש ליצור עקומת כיול.
בתור התחלה, אפס ספקטרופוטומטר UV-vis באמצעות מים מזוקקים ריק כדי לייצג ללא ספיגה. בעת החדרת cuvette לתוך הספקטרופוטומטר, ודא כי הוא מכוון כך האור עובר דרך הצדדים השקופים, וכי רמת הנוזל היא מעל הנתיב של הקרן.
לאחר מכן, להכין 5 מבחנות המכילות את הכרכים המצוינים של כל פתרון מגיב כפי שמוצג בפרוטוקול הטקסט, אשר יניב ריכוזים שונים של המוצר. מכסים כל שפופרת באצבע עם כפפות, ומנערים בעדינות כדי לערבב. אפשר לצינורות לנוח במשך 10 דקות.
השתמש פיפטה פסטר להעביר כמות קטנה של מדגם ריכוז אמצע, פתרון 3, לקובט, ולהניח אותו בספקטרופוטומטר. לרכוש ספקטרום ולרשום את λמקסימום (אורך גל מקסימלי), lambda max, ואת הספיגה שלה. לאחר מכן, החל מהפתרון המדלל ביותר, למדוד את הספיגה של כל הפתרונות הנותרים ב λמקסימום (lambda מקסימום). השתמש באותה cuvette עבור כל המדידות, הקפד לשטוף 3 פעמים בין כל מדגם. חזור על תהליך זה עבור פתרונות 2 – 5.
התווה את הספיגה הנמדדת לעומת ריכוז של תיוציאנט ברזל עבור כל פתרון. קבע את קו ההתאמה הטובה ביותר לנתונים. השיפוע של קו זה הוא מקדם ההנחיה הטוחנת.
כעת, לאחר שנרכשו הנתונים עבור הפתרונות הסטנדרטיים, הכינו ארבע מבינות בינוניות המכילות את אמצעי האחסון המצוינים של פתרונות כפי שמוצג בפרוטוקול הטקסט.
מכסים כל שפופרת באצבע ומנערים בעדינות כדי לערבב. אפשר להם לעמוד לפחות 10 דקות. תקופת מנוחה זו מאפשרת לפתרונות להגיע לשיווי משקל כימי.
השתמש פיפטה פסטר להעביר כמות קטנה של פתרון 6 לקובט, ולהניח אותו בספקטרופוטומטר. לרכוש ספקטרום ולתעד את הספיגה נמדדת ב λהמרביקבוע מראש . חזור על תהליך זה עבור פתרונות 7 עד 9.
לאחר כל הדגימות נמדדו, ניתן לנתח את נתוני הטוחנת והספיגה לפתרונות 1 – 5. עודף גדול של תיוציאנט שימש כדי להבטיח כי כל הברזל הגיב, אשר מפשט את הניתוח.
הנתונים מותווים ליצירת עקומת כיול. אורך הנתיב של האור, l, הוא בדרך כלל 1 ס"מ, וניתן לקחת בחשבון מתוך החישובים. השיפוע של הקו, אשר חושב להיות 7600, ולכן מקדם ההחמצה. עבור פתרונות הבדיקה 6 – 9, ערך זה ואת הספיגה משמשים לחישוב ריכוזי תיוצינאט ברזל בשיווי משקל. עם נתונים אלה, טבלת ICE יכולה להיות מנוצלת לאחר מכן.
ריכוזי התגובה הראשוניים מבוססים על הטוחנות הידועות של ברזל ותיוציאנט שנוספו לפתרון, והנפח הכולל של התגובה. מכיוון שהמוצר נוצר מתגובת 1:1 של ברזל ותיוצינאט, ריכוז שיווי המשקל של כל אחד מהם יורד בכמות המוצר שנוצר. ריכוז שיווי המשקל של כל מין ידוע כיום. ערכים אלה משמשים לחישוב קבוע שיווי המשקל עבור כל פתרון. הערכים קבועים בערך על פני טווח הריכוזים הנחקרים.
המושג של קבוע שיווי המשקל חשוב למגוון רחב של תחומים מדעיים. קבוע שיווי המשקל יכול לשמש כדי לספק מידע שימושי על המידה שבה תגובה תיצור מוצרים לאורך זמן. בדוגמה זו נצפו שתי תגובות המכילות סגול קריסטל.
הפתרון הראשון היה מורכב מגביש סגול ונתרן הידרוקסיד. הצבע נצפה משתנה במהירות מסגול לחסר צבע. תגובה זו יש ערך K גדול מאוד, המציין כי המוצרים טופס כמעט לחלוטין לאורך זמן.
קריסטל סגול הגיב אז עם נתרן אצטט. פתרון זה נותר סגול ללא הגבלת זמן. לתגובה זו יש ערך K נמוך מאוד, ולכן היא אינה מתקדמת במידה משמעותית.
לבסוף, ניתן להשתמש בקבוע הניתוק — סוג מסוים של קבוע שיווי משקל — כדי לתאר התנהגות חלבונים. בדוגמה זו, שינויים במבנה של RNA היו במעקב במאגרי תגובת מגנזיום.
RNA מטוהר היה מעורבב בתמיסה עם ריכוזים ידועים של מגנזיום, והורשה להגיע לשיווי משקל. לאחר מכן, מבנה הרנ"א שנוצר זוהה.
במקרה זה, ריכוזים גבוהים יותר של מגנזיום גרמו לאתרי תגובתי ב- RNA להיות פחות מוגנים, והפיקו Kd שהיה מחצית מהערך.
הרגע צפית בהקדמה של JoVE לנחישות ספקטרופוטומטרית של קבוע שיווי המשקל. עכשיו אתה צריך להבין את מערכת היחסים המוגדרת על ידי חוק באר למברט, כיצד לקבוע ריכוז מספיגה באמצעות ספקטרופוטומטר, וכיצד לחשב קבוע שיווי משקל באמצעות ריכוזי שיווי משקל.
תודה שצפיתם!
Subscription Required. Please recommend JoVE to your librarian.
Results
טבלה 4 מפרטת את נתוני הספיגה והריכוז לפתרונות 1 – 5. ריכוזים של Fe(SCN)2+ נקבעו מהריכוזים הראשוניים של Fe3+ תחת ההנחה שכל Fe3+ מומר ל- Fe(SCN)2 +. עודף גדול של SCN- שימש צינורות 1 - 5 כדי להבטיח כי הנחה זו נכונה.
הטוחנת [Fe(SCN)2+] והספיגה משורטטות באיור 2. הספיגות הנמדדות מסכימות היטב עם החוק של באר.
טבלה 5 מפרטת ספיגות נמדדות וערכי K מחושבים עבור צינורות 6 – 9. ערכי K נקבעו באמצעות שיטת הטבלה ICE. ריכוזי המגיבים הראשוניים התבססו על הטוחנות הידועות של Fe3+ ו- SCN- בפתרונות המגיבים ובנפח הכולל של התגובה (10 מ"ל). ריכוז שיווי המשקל של Fe(SCN)2+ נקבע על ידי חלוקת ספיגה נמדדת על ידי ספיגת הטוחנת של Fe(SCN)2 +. כי כל המוצר נוצר מתגובת 1:1 של Fe3+ ו SCN-, ריכוז שיווי המשקל של Fe(SCN)2+ מתאים לירידה בריכוז המגיבים. טבלה 6 מציגה את התהליך עבור מבחנה 6.
קבוע שיווי המשקל מחושב מהריכוזים בשורת שיווי המשקל. עבור מבחנה 6,
ערך K הממוצע היה 147 ± 11, הממחיש כי K הוא בערך קבוע על פני טווח הריכוזים שנחקרו.
איור 2. גרף קו של ספיגה לעומת ריכוז עבור Fe(SCN)2+.
| צינור | [Fe(SCN)2+] (מול/ל) | ספיגה |
| 1 | 1.00 x 10–5 | 0.10 |
| 2 | 2.00 x 10–5 | 0.20 |
| 3 | 3.00 x 10–5 | 0.25 |
| 4 | 4.00 x 10–5 | 0.32 |
| 5 | 5.00 x 10–5 | 0.42 |
טבלה 4. ספיגה לעומת נתוני ריכוז עבור Fe(SCN)2+.
| צינור | ספיגה | K |
| 6 | 0.120 | 136 |
| 7 | 0.268 | 161 |
| 8 | 0.461 | 142 |
| 9 | 0.695 | 150 |
שולחן 5. ערכי ספיגה נמדדים ו- K מחושב לתגובת ברזל (III) עם תיוציאנט.
| [Fe3+] (מול/ל) | [SCN–] (מול/ל) | [Fe(SCN)2+] (מול/ל) | |
| הראשונית | 3.57 x 10–4 | 3.57 x 10–4 | 0 |
| שינוי | –1.58 x 10–5 | –1.58 x 10–5 | +1.58 x 10–5 |
| שיווי משקל | 3.41 x 10–4 | 3.41 x 10–4 | 1.58 x 10–5 |
שולחן 6. טבלת ICE הממחישה את התהליך המשמש עבור מבחנה 6.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
קבוע שיווי המשקל מספק מידע שימושי על המידה שבה תגובה תמשיך ליצור מוצרים לאורך זמן. תגובות עם ערך גדול של K,גדול בהרבה מ-1, ייצרו מוצרים שכמעט הושלמו בהינתן מספיק זמן(איור 3). תגובות עם ערך של K פחות מ- 1 לא ימשיכו קדימה במידה משמעותית. קבוע שיווי המשקל משמש אפוא כמדד של היתכנות של תגובה כימית.
איור 3. קבוע שיווי המשקל של תגובה זו גדול מ- 1. כמות משמעותית של צורות מוצר צבעוניות בכל מקרה, למרות הריכוזים הראשוניים של מגיבים שונים.
קבוע שיווי המשקל מספק גם מידע תרמודינמי שימושי על השינויים באנרגיה חופשית, אנטלפיה ואנטרופיה במהלך תגובה כימית. קבוע שיווי המשקל קשור לשינוי האנרגיה החופשית של התגובה:
שינוי האנרגיה החופשית של התגובה קשור בתורו לשינויי האנטלפיה והאנטרופיה של התגובה:
מדידות של תלות הטמפרטורה של K יכול לחשוף את שינוי האנטלפיה ΔH ואת האנטרופיה לשנות ΔS לתגובה. בנוסף לספק כימאים עם תובנה על דפוסים בהתנהגות מולקולרית, טבלאות של נתונים תרמודינמיים ניתן להשתמש כדי לזהות תגובות עם תכונות תרמודינמיות חיוביות. לדוגמה, תגובות redox המשחררות כמויות גדולות של אנרגיה (הקשורות לערכי ΔG שליליים) הן מועמדות אטרקטיביות לסוללות.
ערכים של K עבור תגובות דיסוציאציה חומצה (Kערכים) שימושיים לחיזוי התוצאות של תגובות בסיס חומצה, אשר נשלטים תרמודינמית. חומצות חזקות קשורותלערכי Kגדולים וחומצות חלשות עםערכי Kקטנים. מחווני pH הם חומצות חלשות עם צורות חומציות בסיסיות וצבעוניות שונות, וה- pKa (הלוגריתם השלילי של Ka) של מחוון מייצג את ה- pH שבו מתרחש שינוי צבע כחומצה או בסיס נוסף לפתרון המחוון.
באופן דומה, Ka ערכים משמשים להכנת פתרונות מאגר כדי להשיג ערך pH היעד. ה- pKa של חומצה חלשה מייצג את החומציות שבה החומצה והבסיס המ מצומד שלה נמצאים בתמיסה בריכוזים שווים. כאשר כמויות שוות של חומצה חלשה ובסיסה מצומד מומסים בתמיסה, ה- pH של הפתרון שווה ל- pKa של החומצה החלשה.
Subscription Required. Please recommend JoVE to your librarian.
