12.10:
凝固点降下と沸点上昇
12.10:
凝固点降下と沸点上昇
沸点上昇
液体の沸点とは、液体の蒸気圧が大気圧と等しくなる温度のことです。不揮発性の溶質があると蒸気圧が下がるため、溶液の沸点は上昇します。蒸気圧は温度によって上昇するため、大気と同等の蒸気圧を得るためには、純溶媒よりも高い温度が必要となります。不揮発性の溶質が溶媒に溶解したときに観測される沸点の上昇は、沸点上昇と呼ばれ、溶質種のモル濃度に正比例します。
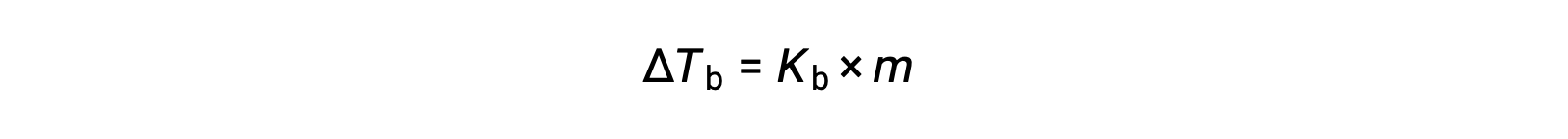
ここで、Kbは沸点上昇定数であり、mは全ての溶質種のモル濃度(molality)です。沸点上昇定数の大きさは、溶媒の種類に依存します。
凝固点降下
溶液は純粋な液体よりも低い温度で凍結します。この現象を利用して、道路や歩道の氷を塩、塩化カルシウム、尿素などで溶かす除氷システムや、自動車のラジエーターにエチレングリコールを“不凍液”として使用されています。海水は淡水よりも低い温度で凍るため、北極や南極の海は0°C以下でも凍らない(海に生息する魚などの変温動物の体液も同様である)。
純粋な溶媒の凝固点と比較した希薄溶液の凝固点の減少、 ΔTf は凝固点降下と呼ばれ、溶質のモル濃度に正比例します。
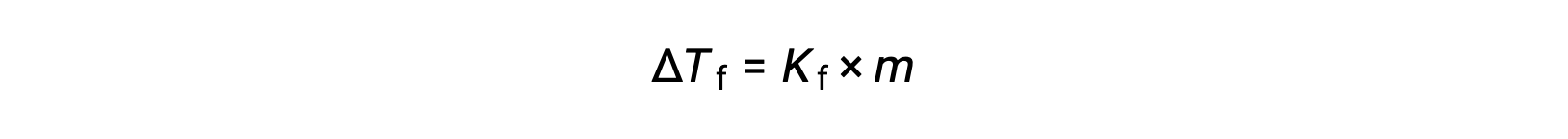
ここで、mは溶質のモル濃度、Kfは凝固点降下定数と呼ばれます。沸点上昇定数と同様に、これらの値は溶媒の種類に依存します。
モル質量の決定
浸透圧や凝固点、沸点、蒸気圧の変化は、一定量の溶液中に存在する溶質種の数に正比例します。したがって、既知の質量の溶質を用いて調製した溶液について、これらの特性のいずれかを測定すれば、その溶質のモル質量を決定することができます。
例えば、4.00 gの非電解質を55.0 gのベンゼンに溶かした溶液は、2.32 °Cで凍ることがわかります。理想的な溶液挙動を仮定すると、この化合物のモル質量はどのくらいになるのでしょうか?
この問題を解くには、まず、観測された凝固点と純粋なベンゼンの凝固点からの凝固点の変化を計算します。
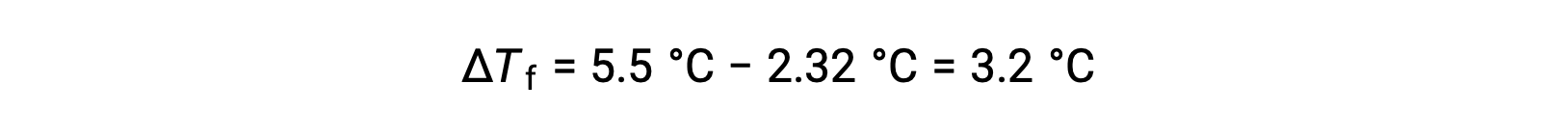
続いて、ベンゼンの凝固点降下定数であるKfと ΔTfからモル濃度を求めます。
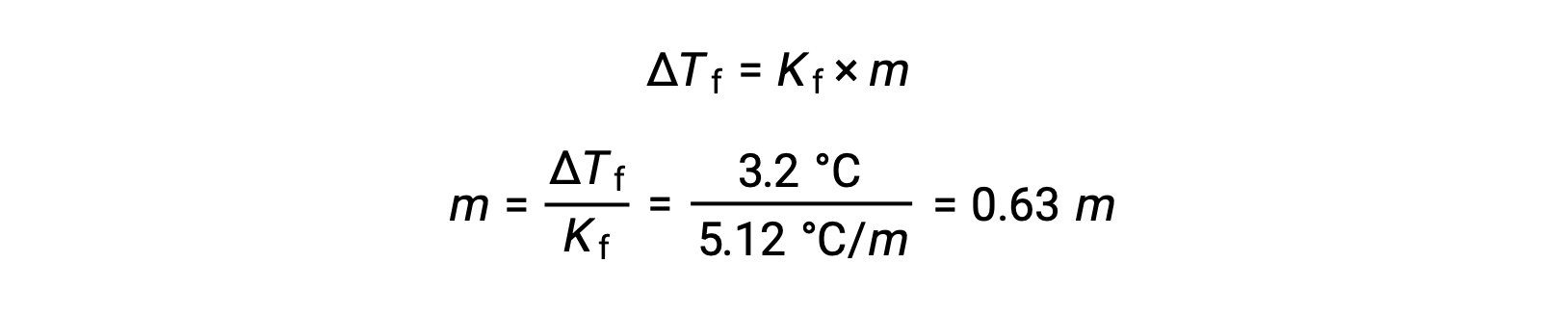
次に、モル濃度と溶液を作るのに使用した溶媒の質量から、溶液中の化合物のモル数を求めます。
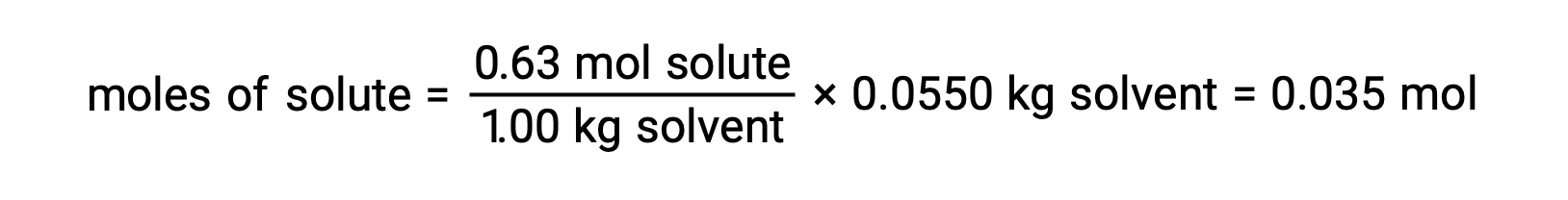
そして最後に、溶質の質量からモル質量を求め、その質量に含まれるモル数を求めます。
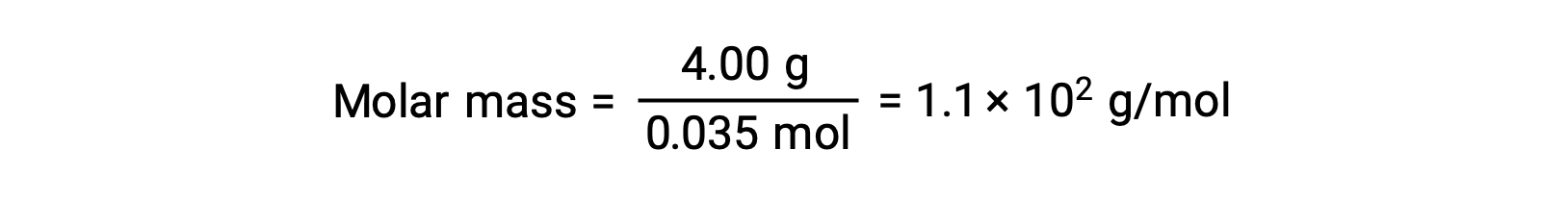
上記の文章は以下から引用しました。Openstax, Chemistry 2e, Section 11.4: Colligative Properties.
Suggested Reading
- Steffel, Margaret J. "Raoult's law: A general chemistry experiment." Journal of Chemical Education 60, no. 6 (1983): 500.
- Berka, Ladislav H., and Nicholas Kildahl. "Experiments for Modern Introductory Chemistry: Intermolecular Forces and Raoult's Law." Journal of chemical education 71, no. 7 (1994): 613.
