Overview
资料来源: 亚历山大的贾斯汀和马赫迪。宾夕法尼亚州立大学机械与核工程系
当液体沿着明渠高速流动时, 水流会变得不稳定, 轻微的扰动会使液体上表面突然向更高的水平过渡 (图 1a)。这种急剧增加的液位称为水力跳跃。液位的增加会导致平均流速的降低。因此, 潜在的破坏性流体动能耗散为热。水力跃迁被故意地被设计入大水工作, 例如水坝溢洪道, 防止损伤和减少可能由快速的移动的小河造成的侵蚀。水力跃迁在河和小河也自然地发生, 并且可以被观察在家庭情况, 例如水的辐形流出从水龙头到水槽 (图 1b)。
在这个项目中, 将建立一个明渠流动实验设施。将安装一个闸门, 该闸门是可以升降的垂直闸门, 用来控制上游水库到下游溢洪道的水流流量。将测量在闸门出口处产生水力跃迁所需的流量。这些研究结果将与基于质量和动量分析的理论值进行比较。
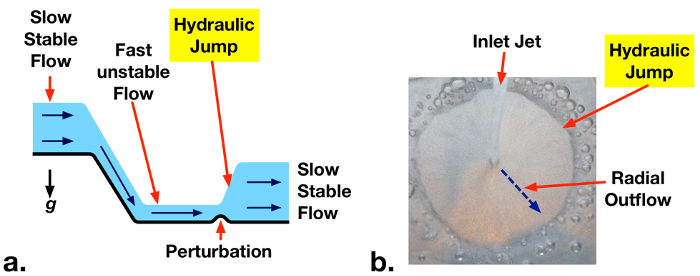
图 1: a. 由于对不稳定的高速水流的轻微扰动, 从溢洪道下游发生的水力跃迁。水力跃迁的例子在水的辐形流出从家庭水龙头。
Principles
在宽阔的明渠水流中, 液体只被一个较低的固体边界所限制, 其上表面暴露在大气中。控制容积分析可以在明渠流量的一段上进行, 以平衡质量和动量的入口和出口运输 (图 2)。如果速度在控制音量 (V1和V2分别) 的入口和出口处具有相同的液体深度h1和h2, 则稳定的质量流量平衡减少到:
 (1)
(1)
此控制容积的x方向动量分析与入口和出口动量流率 (Eqn 2) 的静水压压力 (由于流体深度) 的作用力。压力作用力作用于控制容积的两侧, 并与液体的比重相等 (液体密度乘以重力加速度: ρg), 乘以每边的平均液体深度 (H1/2,H2/2), 乘以压力作用在每一侧的高度 (h1, h2)。这导致 Eqn 左侧的二次表达式2。动量流速通过每边 (Eqn. 2, 右边) 是相等的液体的质量流速通过控制容量 (在:, 出:) 乘以流体速度 (  v
v  1, v2)。
1, v2)。
 (2)
(2)
Eqn 1 可以替换为 Eqn 2 以消除V2。德数 () 也可以被替换, 这代表了流入流体动量与静力的相对强度. 生成的表达式可以表示为:
生成的表达式可以表示为:
 (3)
(3)
这个立方方程有三解。一个是 H1 = H2, 给正常开放渠道行为 (入口深度 = 出口深度)。第二个解决方案给出了一个负的液位, 这是物理, 可以消除。剩下的解决方案允许增加深度 (水力跃迁) 或减少深度 (水力消沉), 根据入口德数字。如果入口德数 (Fr1) 大于 1, 则该流称为超临界 (不稳定) 并且具有较高的机械能 (动能 + 引力势能)。在这种情况下, 水力跃迁可能形成自发地或由于对流动的一些干扰。水力跃迁将机械能转化为热能, 大大降低了动能, 并略微增加了流动的势能。所产生的出口高度由 Eqn 4 (Eqn. 3 的解决方案) 给出。如果 Fr1 > 1, 因为它会增加流动的机械能, 违反热力学第二定律, 就无法发生液压凹陷。
 (4)
(4)
水力跃迁的力量增加与入口德数字。当 Fr1增加时, h2/h1的大小会增加, 而入口动能的较大部分则作为热 [1] 消散。

图 2: 包含液压跃迁的明渠水流段的控制容积。指出了每单位宽度的进、出质量和动量流率。每个单位宽度的静水压力在下图中表示。
Procedure
注: 本实验采用了相对强大的潜水泵。泵只应插入 GFCI 插座, 以尽量减少电气风险。确保在实验附近没有其他的/C 供电的设备在运行。
1. 明渠流量设施和水箱的制作 (见图和照片, 图 3)
- 切割长度〜6.0 毫米厚 x 9.5 厘米宽透明丙烯酸板的长度如下: 2×15厘米, 2×25厘米, 1×34厘米, 1×41厘米 (图 3a)。建议使用桌锯或激光切割机, 以确保边缘相对平坦, 且纸张厚度相等。
- 在两个 60 x 45 cm 丙烯酸板的右下角切孔, 以安装流量计 (图 3a)。在前板的右上角切一个孔, 安装流量控制阀。
- 使用丙烯酸水泥 (例如, SCIGRIP 16) 来粘合丙烯酸板, 如图3a 所示。在处理丙烯酸水泥时, 确保充分通风和佩戴手套。在固化过程中, 将水泥与注射器一起应用, 并使用掩蔽带来定位面板是很有帮助的。让水泥固化 24-48 小时。
- 将流量计安装在前面板上, 并用所提供的螺钉进行粘贴。安装1《不扩散条约》, ½不扩散条约减少流量计进口和出口港口的配件。安装½不扩散条约0.5 在. 内径带刺配件适配器。
- 安装 0.5 in。身份证和0.75。在闸阀 (流量控制) 上安装有带刺的标识。用20厘米长的油管将带刺的装置连接到潜水泵上, 使阀门手柄与丙烯酸外壳的右上角的孔相连 (图 3 b-c)。
- 将泵插入下部蓄水池, 安装阀门, 使阀杆通过安装孔, 手柄位于机箱外 (图 3c)。
- 在流动装置的入口部分附近插入一个垂直的亚克力面板, 使其下方有大约5.0 毫米的开口 (图 3 b-c)。该组件将充当闸门, 并可以提高和降低到控制从上层水库流向通道的流量。
- 用不锈钢羊毛精练垫将上部蓄水池松散地填满。这有助于在通道中均匀分布进水水流。
- 将阀门出口连接到流量计入口, 并配有长度的软塑料油管。用塑料管将流量计出口连接到上水库。确保上部油藏的油管入口很好地锚定, 以便在泵开启时不会摆动。
- 用清水填满下层水库。
2. 执行实验
- 使用标尺测量栅极下面的间隙高度, 并将值表示为H1。
- 打开泵, 并调整流量使用阀门的各种流速 (5-15 升 min-1)。使用标尺测量每种情况下从门 (H2) 下游的液体深度。
- 定性地观察在不同流速下形成的水力跃迁的形状。观察液压跃迁形成的最小阈值流速。更清晰、更大的振幅 (H2 -h1), 应在较高的流量下进行跳转。
3. 数据分析
- 对于每个流率大小写, 计算入口速度, V1, 从容积流速。其中是卷流速率,

 W是通道宽度。
W是通道宽度。 - 计算每个案例的入口德数 () 和理论下游液体深度 (Eqn. 4).
 将这些值与测量的下游跳转深度进行比较。
将这些值与测量的下游跳转深度进行比较。

图 3: a. 设施结构示意图和尺寸. 液压跃迁装置的流程图. 标记实验设备的照片。
水力跃迁是一种现象, 发生在快速流动的开放流动时, 流量变得不稳定。当跳跃发生时, 液体表面的高度会突然增加, 导致深度增加, 下游的平均流速下降。这一现象的一个重要的副作用是, 上游流动中的大部分动能都是作为热能消散的。虽然水力跃迁经常自然地出现, 例如在河或流动入家庭水槽, 他们也被故意地被设计入大自来水厂减少侵蚀或增加混合。这段视频将说明液压跳跃在一个直通道背后的原理, 然后用一个小规模的明渠流设施来实验演示这种现象。在分析结果的基础上, 讨论了液压跳跃的一些应用。
考虑流动在一个宽广, 平直的部分在一个开放渠道在水力跃迁发生和构造控制容量在闸附近在跃迁。如果流速在入口和出口处是均匀的, 那么质量守恒就会产生上游和下游流体深度之间的简单关系。深度乘以速度是恒定的。通过考虑动量守恒, 可以找到第二个关系。通过输入和输出的质量传输动量与相应的质量通量乘以流速。控制容积表面的静液力也有助于动量平衡, 必须包括在内。这些力等于表面的平均压强乘以面积。在这一点上, 它是有用的介绍德数字, 一个无量纲数量命名以英国工程师和 hydrodynamicist, 威廉德。德数的特征是流体动量相对于静力的强度。现在, 如果动量关系被改写为德数, 随着输出速度被淘汰的质量关系, 结果是一个立方方程, 从下游和上游的比值的深度。这一方程可以通过分解出上游和下游深度相等的琐碎解来简化。利用二次方程可以很容易地找到剩下的两个解, 但由于非物理的原因, 否定解可被消除。剩余的解答对应于深度的增量, 水力跃迁, 或者减少深度, 水力消沉, 根据上游德数字的价值。如果上游德数大于 1, 则该流具有较高的机械能, 且超临界或不稳定。液压凹陷不能在这一制度中形成, 因为它会增加机械能, 违反热力学第二定律。另一方面, 水力跃迁可以形成, 自发地或由于有些干扰在流程。一个输入德数代表一个水力跃迁的起始的最低阈值。水力跃迁将机械能耗散为热能, 并显著降低动能, 同时略增势能的流动。随着德数的增加, 下游向上游深度的比值和动能耗散的热量。现在我们了解了液压跃迁的原理, 让我们在实验中对它们进行检验。
首先, 按照文中所述, 制作明渠流量装置。该设施有一个由开放通道连接的上、下水库。从下部储层抽水的水在上部储层中沉积, 流量由阀门和流量计测量, 并与泵配合。上部储层中的钢质羊毛有助于均匀地将水分布在剖面的宽度上, 而可调节的闸门则在进入通道时控制流体的深度。流经通道后, 流体被沉积回下部油藏。当流动设施被装配时, 将其设置在长凳上, 并卸下附近的电子设备。将泵塞入 GFCI 出口, 使触电的风险降到最低, 然后用清水填满下部蓄水池。你现在已经准备好进行实验了。
将闸门调整到大约五毫米。用直尺测量水闸下方缝隙的最终高度, 并记录此距离为上游水流深度, H1。当您完成后, 打开泵和使用阀门, 以最大限度的流量, 而不超过流量表的规模。再次使用标尺测量液压跃迁后的流体深度。记录流量, 并与这第二个距离, 这是下游流的深度, H2。在继续之前, 观察水力跃迁的形状。你应该注意到更大, 更突然的转变, 更高的流速, 和更小, 更渐进的转变, 以较低的流量率。现在, 重复您的测量和观察为连续地更低的流速。尝试确定水力跃迁形成的最小阈值流速。一旦找到了阈值流率, 就可以分析结果了。
对于每一个容积流速, 你应该有一个下游流体深度的测量。在所有情况下, 上游深度是相同的。完成每个测量的以下计算, 并在一路上传播不确定性。首先, 确定入口流速。将容积流速除以通道宽度和上游深度。接下来, 使用前面给出的定义来计算上游的德数, 并以重力的加速度代替, 以及上游的高度和速度。现在, 利用德数和非平凡解的跳跃高度来计算理论的下游深度。将理论预测与实测的下游深度进行比较。在超临界流速下, 这些预测与实验不确定范围内的测量深度相匹配。查看您的阈值流速的结果。在实验的不确定性, 德数字是一个, 正如我们预期从理论分析。通过水力跃迁的机械能损失率也可以从这些数据中计算出来。首先, 计算流体进入跃迁的机械能, 即入口的动能和势能流速的总和。现在, 以同样的方式确定输出能量的速率, 但在出口处有值。机械能耗散到热的速率是输入和输出速率之间的差异。在这个实验中, 能量损失率可以达到大约40% 的进口能量, 或更高。这些结果突出了动量分析和规模模型实验对液压系统行为的理解和预测的有效性。现在, 让我们来看看其他一些方法, 水力跳跃的使用。
液压跳跃是一种重要的自然现象, 具有许多工程应用。水力跃迁经常被设计入液压系统驱散液体机械能入热。这就降低了溢洪道高速液体射流对损伤的可能性。在高通道流速下, 沉积物可以从河床和流化中抬升。通过降低流速, 水力跃迁也减少了桩周围的侵蚀和冲刷的可能性。在水处理装置中, 水力跃迁有时用于诱导混合和通气流动。在实验中可以定性地观察水力跃迁的混合性能和气体夹带。
你刚才看了朱庇特介绍液压跳跃现在, 您应该了解如何使用控制卷方法来预测流行为, 以及如何使用开放式通道流工具来测量此行为。在实际应用中, 你也看到了工程液压跃迁的一些实际用途。谢谢收看
Results
表1总结了上游德数 (Fr1) 以及测量和理论下游深度。水力跃迁的形成的被测量的门限入口流速对应于法郎1 = 0.9 ± 0.3, 匹配理论价值1。在超临界流速 (Fr1 > 1) 预测下游深度匹配理论值 (Eqn 4) 在实验的不确定性。
表 1-测量的上游德数字 (Fr1) 和下游液体深度为H1 = 5 ± 1 mm
|
液流率
(, |
上游德编号 (Fr1) | 测量的下游深度 (H2) | 预测下游深度 (H2) | 注意 |
| 6.0 ± 0。5 | 0.9 ± 0。3 | 5 ± 1 | 5 ± 1 | 水力跳跃的门限德数 |
| 11.0 ± 0。5 | 1.7 ± 0。5 | 11 ± 1 | 10 ± 2 | |
| 12.0 ± 0。5 | 1.9 ± 0。6 | 12 ± 1 | 11 ± 2 | |
| 13.5 ± 0。5 | 2.1 ± 0。6 | 14 ± 1 | 13 ± 2 |
在图4中介绍了上述情况下液压跃迁的照片。未观察到 = 6.0 l 最小 -1 (Fr1 = 0.9) 的跳转。在其他两种情况下, 都有跳转1 > 1。在较高的流量超临界情况下, 观测到更强、高振幅的跃迁。
-1 (Fr1 = 0.9) 的跳转。在其他两种情况下, 都有跳转1 > 1。在较高的流量超临界情况下, 观测到更强、高振幅的跃迁。

图 4: 水力跃迁的相片, 显示重要情况 (没有跳跃, 法郎1 = 0.9) 和跳跃在法郎1 = 1.9, 2.1.
Applications and Summary
实验证明了在明渠水流中, 在超临界条件下 (Fr > 1) 形成的水力跃迁现象。建立了实验装置, 以观察不同流速下的水力跳跃现象。对下游液体深度进行了测量, 并与理论预测相匹配。
在这个实验中, 最大报告的入口德数是2.1。该泵额定提供显著较高的流速, 但阻力在流量表有限的可测量流量为〜14升 min-1。在未来的实验中, 一个更大的头额定或较低的压力下降流量表的泵可以使更广泛的研究条件。
水力跃迁经常被设计入液压系统驱散液体机械能入热。这就降低了溢洪道高速液体射流对损伤的可能性。在高通道流速下, 沉积物可以从河床和流化中抬升。通过降低流速, 水力跃迁也减少了桩周围的侵蚀和冲刷的可能性。在水处理装置中, 水力跃迁有时用于诱导混合和通气流动。在实验中可以定性地观察水力跃迁的混合性能和气体夹带。
对于所有这些应用, 跨水力跃迁的动量分析, 如这里所讨论, 是预测液压系统行为的关键工具。类似的, 规模模型实验, 如在本项目中展示的, 可以指导设计的明渠流几何和液压设备的大型工程应用。
References
- Cimbala, Y.A. Cengel, Fluid Mechanics Fundamentals and Applications, 3rd edition, McGraw-Hill, New York, NY, 2014.





