7.8: The Uncertainty Principle
Werner Heisenberg considered the limits of how accurately one can measure properties of an electron or other microscopic particles. He determined that there is a fundamental limit to how accurately one can measure both a particle’s position and its momentum simultaneously. The more accurate the measurement of the momentum of a particle is known, the less accurate the position at that time is known and vice versa. This is what is now called the Heisenberg uncertainty principle. He mathematically related the uncertainty in the position and the uncertainty in momentum to the quantity involving Planck’s constant.
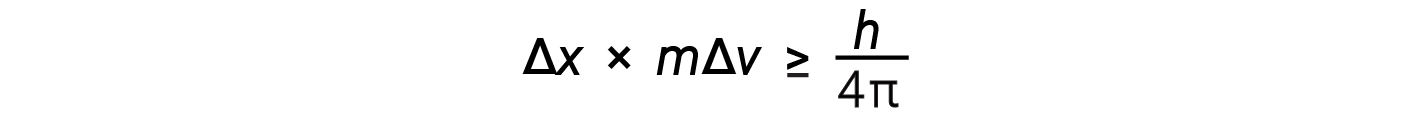
This equation calculates the limit to how precisely one can know both the simultaneous position of an object and its momentum.
Thus, the more accurate is the position of the electron, the less accurate is its velocity and vice versa. For example, one can predict where a baseball would land in the outfield by noting its initial position and velocity and by considering the effect of gravity and wind, etc. The trajectory of the baseball can be estimated.
For an electron, however, the position and velocity cannot be determined simultaneously. Therefore, a trajectory for the electron of an atom cannot be determined. This behavior is indeterminate. Instead of the precise location of an electron, one can talk in terms of the probability of finding an electron in a certain region of the atom, which is a probability density. It can be indicated as psi square (ψ2). The higher the probability of finding an electron in a particular region, the larger the value of psi square. Based on this, atoms are described as consisting of a nucleus surrounded by an electron cloud.
Heisenberg’s principle imposes ultimate limits on what is knowable in science. The uncertainty principle can be shown to be a consequence of wave–particle duality, which lies at the heart of what distinguishes modern quantum theory from classical mechanics.
This text is adapted from Openstax, Chemistry 2e, Section 6.3: Development of Quantum Theory.


