19.4: Energia de Ligação Nuclear
A diferença entre as massas calculadas e medidas experimentalmente é conhecida como defeito de massa do átomo. No caso do hélio-4, o defeito de massa indica uma “perda” em massa de 4,0331 amu – 4,0026 amu = 0,0305 amu. A perda de massa que acompanha a formação de um átomo de protões, neutrões, e eletrões deve-se à conversão dessa massa em energia que se transforma à medida que o átomo se forma. A energia de ligação nuclear é a energia produzida quando os nucleões dos átomos estão ligados entre si; esta é também a energia necessária para dividir um núcleo nos seus protões e neutrões constituintes. As mudanças energéticas associadas às reações nucleares são muito maiores do que as das reações químicas.
A conversão entre massa e energia é representada de forma mais identificável pela equação de equivalência de massa–energia, como afirmado por Albert Einstein: E = mc2, onde E é energia, m é massa da matéria a ser convertida, e c é a velocidade da luz em vácuo. Utilizando esta equação de equivalência de massa–energia, a energia de ligação nuclear de um núcleo pode ser calculada a partir do seu defeito de massa. Uma variedade de unidades é geralmente utilizada para energias de ligação nuclear, incluindo eletrão-volts (eV), com 1 eV a igualar a quantidade de energia necessária para mover a carga de um eletrão através de uma diferença de potencial elétrico de 1 volt: 1,602 × 10–19 J.
Para calcular a energia de ligação a partir do defeito de massa, em primeiro lugar, exprime-se o defeito de massa em g/mol. Isto é feito facilmente considerando a equivalência numérica da massa atómica (amu) e da massa molar (g/mol) que resulta das definições das unidades amu e mole. O defeito de massa para He-4 é, portanto, 0,0305 g/mol. Para acomodar as unidades dos outros termos na equação de massa–energia, a massa deve ser expressa em quilogramas, uma vez que 1 J = 1 kg m2/s2. A conversão de gramas em quilogramas produz um defeito de massa de 3,05 × 10–5 kg/mol. Substituindo esta quantidade na equação de equivalência de massa–energia produz:
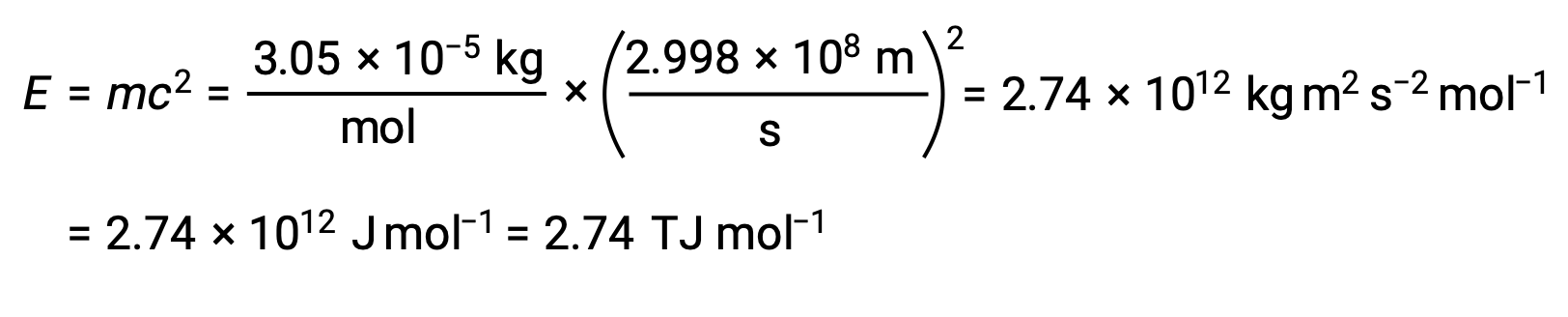
A energia de ligação para um único núcleo é calculada a partir da energia de ligação molar utilizando o número de Avogadro:
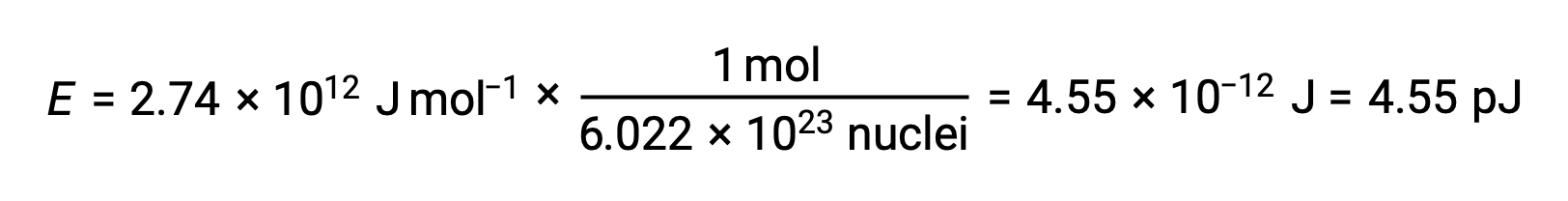
Lembre-se que 1 eV = 1,602 × 10–19 J. Utilizando a energia de ligação calculada:
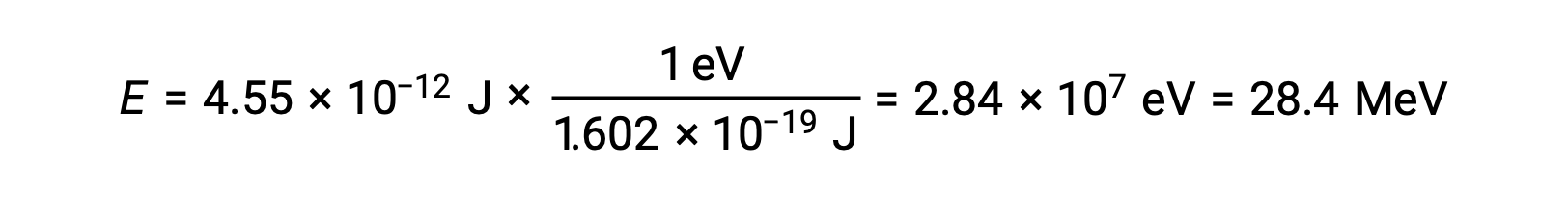
A estabilidade relativa de um núcleo está correlacionada com a sua energia de ligação por nucleão, a energia de ligação total para o núcleo dividida pelo número de nucleões no núcleo. Por exemplo, a energia de ligação para um núcleo de hélio-4 é de 28,4 MeV. A energia de ligação por nucleão para um núcleo de hélio-4 é, portanto:
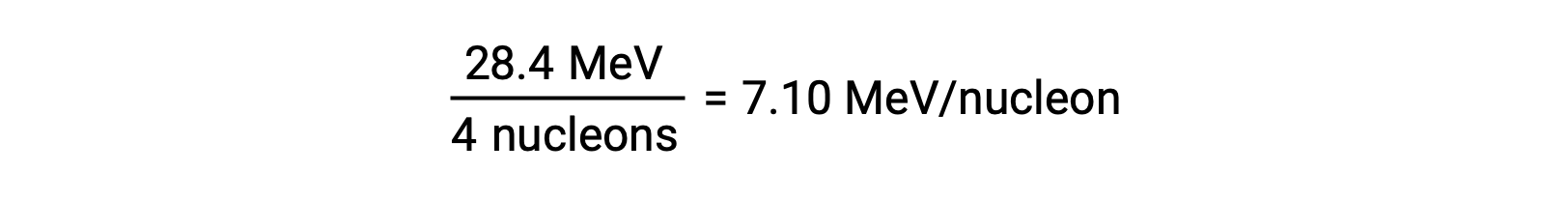
A energia de ligação por nucleão é maior para nuclídeos com um número de massa de aproximadamente 56.
Este texto é adaptado de Openstax, Chemistry 2e, Section 21.1: Nuclear Structure and Stability.


