20.9: Crystal Field Theory - Tetrahedral and Square Planar Complexes
Tetrahedral Complexes
Crystal field theory (CFT) is applicable to molecules in geometries other than octahedral. In octahedral complexes, the lobes of the dx2−y2 and dz2 orbitals point directly at the ligands. For tetrahedral complexes, the d orbitals remain in place, but with only four ligands located between the axes. None of the orbitals points directly at the tetrahedral ligands. However, the dx2−y2 and dz2 orbitals (along the Cartesian axes) overlap with the ligands less than the dxy, dxz, and dyz orbitals. By analogy with the octahedral case,the energy diagram for the d orbitals in a tetrahedral crystal field can be predicted as shown in Figure 1. To avoid confusion, the octahedral eg set becomes a tetrahedral e set, and the octahedral t2g set becomes a t2 set.
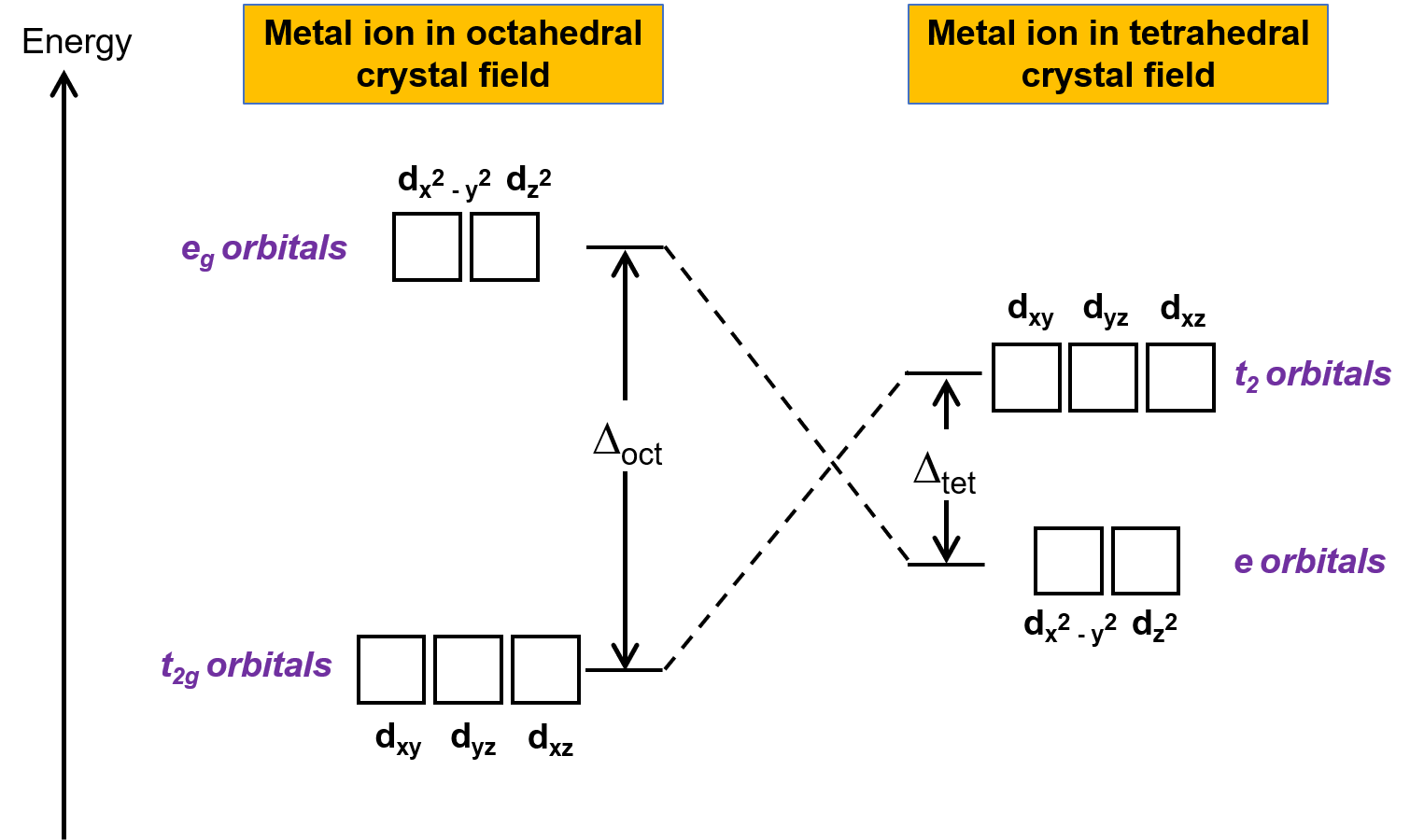
Figure 1. Splitting of the d orbitals of the metal ion under octahedral and tetrahedral crystal fields. In comparison to the octahedral crystal field, the splitting pattern in the tetrahedral crystal field is inverted. The crystal field splitting energy of the octahedral complex, or Δoct, is larger than the crystal field splitting energy of tetrahedral complex, Δtet .
Since CFT is based on electrostatic repulsion, the orbitals closer to the ligands will be destabilized and raised in energy relative to the other set of orbitals. The splitting is less than for octahedral complexes because the overlap is less, so the crystal field splitting energy, or Δtet is usually small.
Square Planar Complexes
The other common geometry is square planar. It is possible to consider a square planar geometry as an octahedral structure with a pair of trans ligands removed. The removed ligands are assumed to be on the z-axis. This changes the distribution of the d orbitals, as orbitals on or near the z-axis become more stable, and those on or near the x- or y-axes become less stable. This results in the octahedral t2g and the eg sets splitting and gives a more complicated splitting pattern (Figure 2).
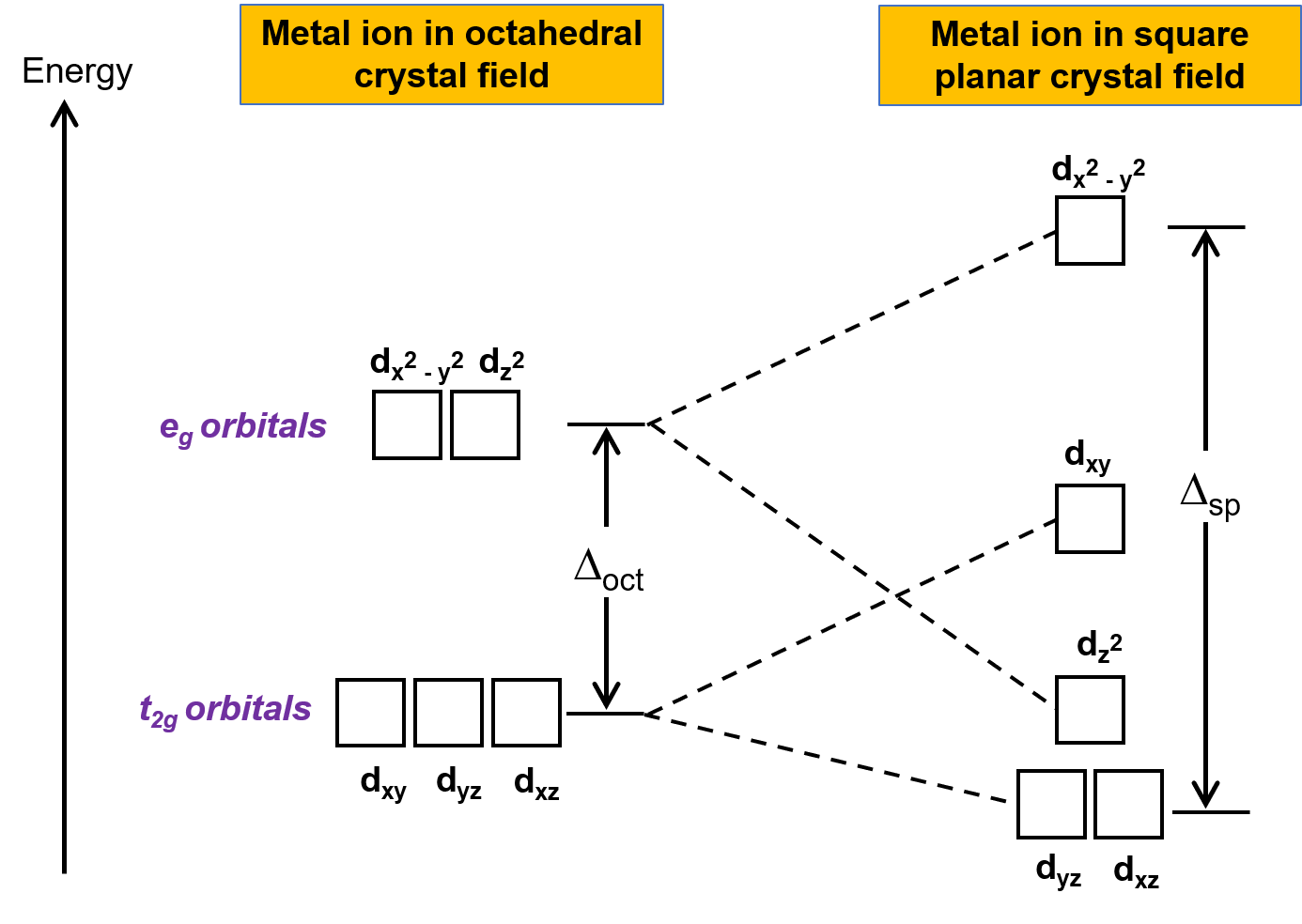
Figure 2. Splitting of the t2g set and the eg set of orbitals in a square planar crystal field. The crystal field splitting energy of square planar complexes, or Δsp, is larger than Δoct.
This text is adapted from Openstax, Chemistry 2e, Section 19.3: Spectroscopic and Magnetic Properties of Coordination Compounds.


