17.6: ギブス自由エネルギー
熱力学の第二法則を用いて、ある過程が自発的かどうかを判断する際の課題の1つは、系のエントロピー変化および外界のエントロピー変化の測定です。しかし、19世紀後半にアメリカの数学者ジョサイア・ウィラード・ギブズが、系の特性のみで定義される新しい熱力学的特性を用いた別のアプローチを導入しました。この新しい性質はギブズ自由エネルギー(G)(または単に自由エネルギー)と呼ばれ、系のエンタルピーとエントロピーの観点から次のように定義されます。
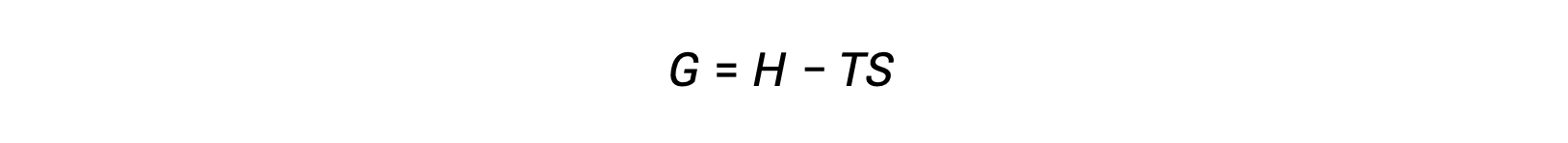
自由エネルギーは状態関数であり、温度と圧力が一定の場合、自由エネルギーの変化( ΔG )は次のように表すことができます。
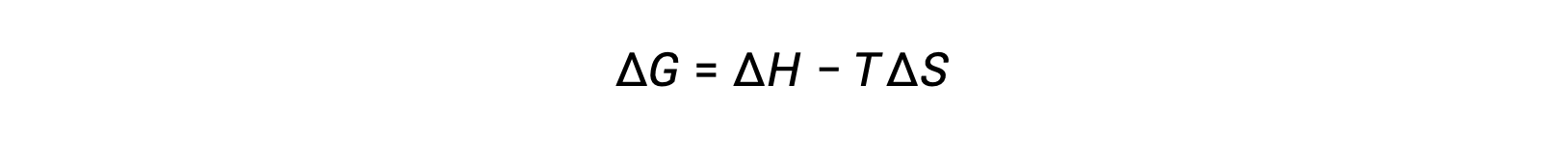
この系の特性と過程における自発性との関係は、先に導いた第二法則の式によって理解できます。
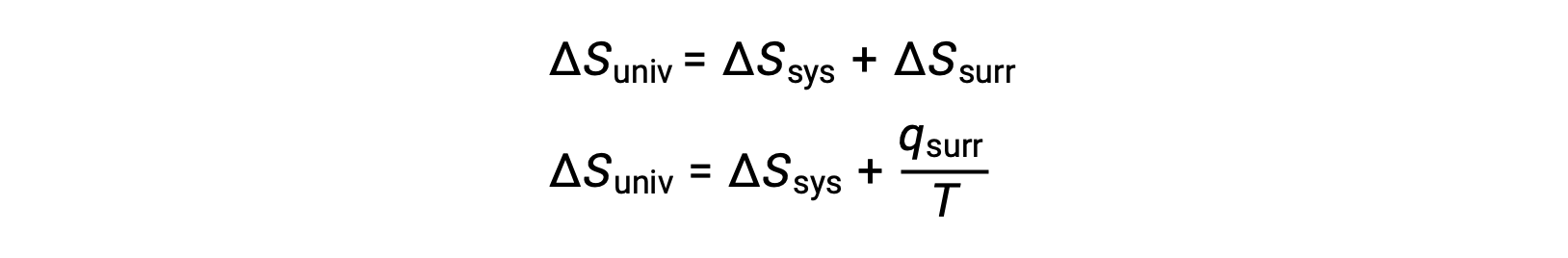
第一法則では、qsurr = −qsysとなり、一定の圧力ではqsys = ΔHとなるので、この式は次のように書き換えることができます。
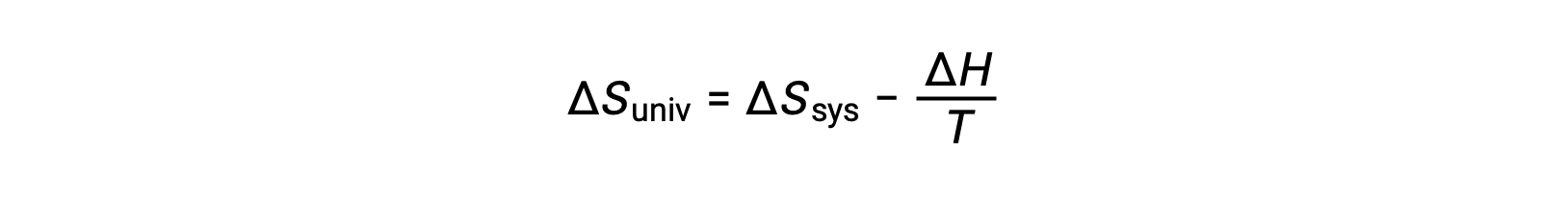
この式の両辺に −T を掛けて並べ替えると、次のようになります。
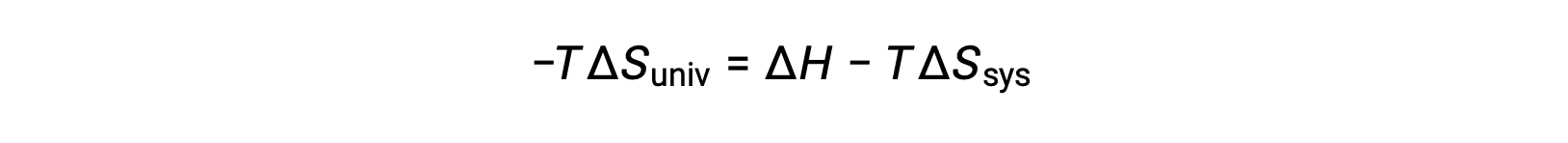
簡単にするために、添え字の “sys”を省略すると、次のような式になります。
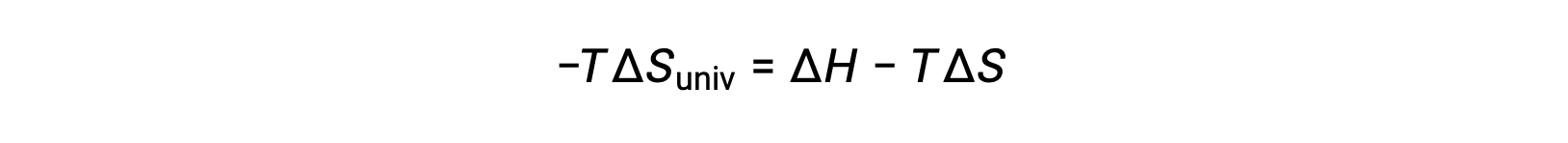
この式を先ほどの自由エネルギー変化の式と比較すると、次のような関係になります。
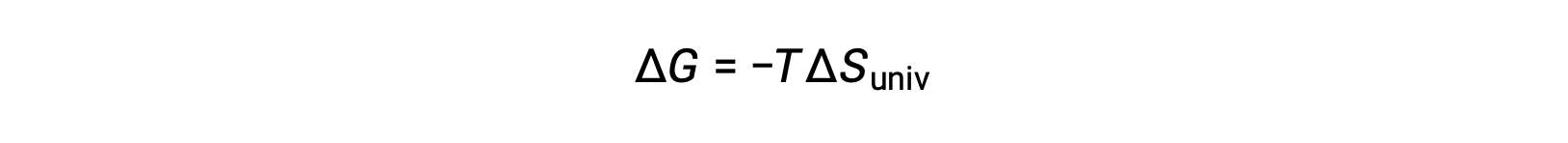
自由エネルギー変化は、以前に定義された自発性の指標である ΔSunivと直接関係しているため、プロセスの自発性を示す信頼可能な指標となります。
ΔSuniv > 0の場合、 ΔG < 0であり、自発的な反応となります。
ΔSuniv < 0の場合、 ΔG > 0であり、非自発的な反応となります。
ΔSuniv = 0の場合、 ΔG = 0であり、反応は平衡状態です。
上記の文章は以下から引用しました。Openstax, Chemistry 2e, Chapter 16.4: Free Energy.


