19.4: Nuclear Binding Energy
The difference between the calculated and experimentally measured masses is known as the mass defect of the atom. In the case of helium-4, the mass defect indicates a “loss” in mass of 4.0331 amu – 4.0026 amu = 0.0305 amu. The loss in mass accompanying the formation of an atom from protons, neutrons, and electrons is due to the conversion of that mass into energy that is evolved as the atom forms. The nuclear binding energy is the energy produced when the atoms’ nucleons are bound together; this is also the energy needed to break a nucleus into its constituent protons and neutrons. The energy changes associated with nuclear reactions are vastly greater than are those for chemical reactions.
The conversion between mass and energy is most identifiably represented by the mass–energy equivalence equation as stated by Albert Einstein: E = mc2, where E is energy, m is mass of the matter being converted, and c is the speed of light in a vacuum. Using this mass–energy equivalence equation, the nuclear binding energy of a nucleus may be calculated from its mass defect. A variety of units are commonly used for nuclear binding energies, including electronvolts (eV), with 1 eV equaling the amount of energy necessary to move the charge of an electron across an electric potential difference of 1 volt: 1.602 × 10–19 J.
To calculate the binding energy from the mass defect, first, express the mass defect in g/mol. This is easily done considering the numerical equivalence of atomic mass (amu) and molar mass (g/mol) that results from the definitions of the amu and mole units. The mass defect for He-4 is therefore 0.0305 g/mol. To accommodate the units of the other terms in the mass–energy equation, the mass must be expressed in kilograms, since 1 J = 1 kg m2/s2. Converting grams into kilograms yields a mass defect of 3.05 × 10–5 kg/mol. Substituting this quantity into the mass–energy equivalence equation yields:
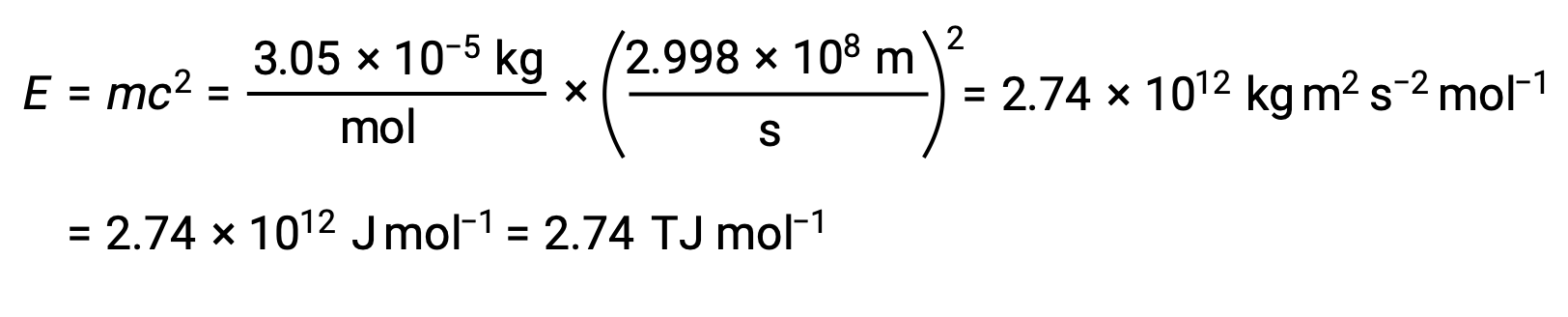
The binding energy for a single nucleus is computed from the molar binding energy using Avogadro’s number:
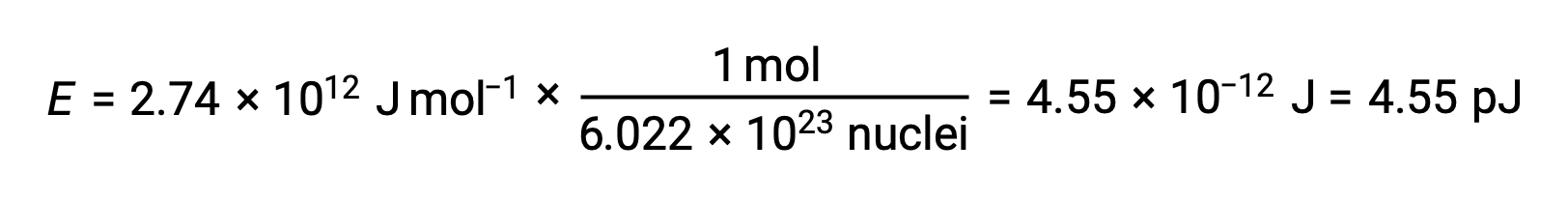
Recall that 1 eV = 1.602 × 10–19 J. Using the binding energy computed:
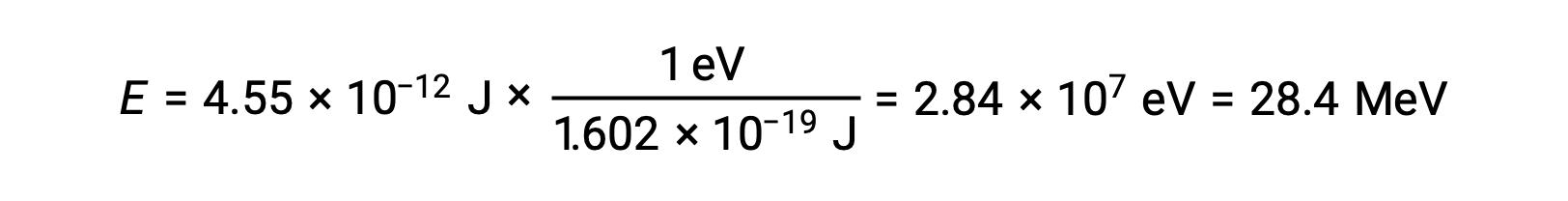
The relative stability of a nucleus is correlated with its binding energy per nucleon, the total binding energy for the nucleus divided by the number of nucleons in the nucleus. For instance, the binding energy for a helium-4 nucleus is 28.4 MeV. The binding energy per nucleon for a helium-4 nucleus is therefore:
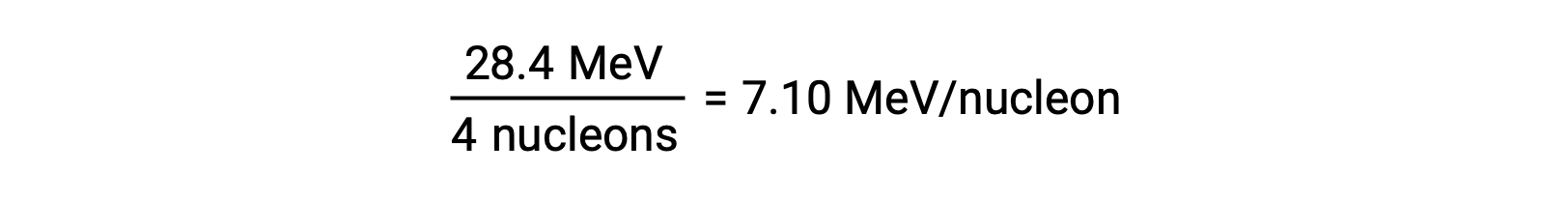
The binding energy per nucleon is largest for nuclides with a mass number of approximately 56.
This text is adapted from Openstax, Chemistry 2e, Section 21.1: Nuclear Structure and Stability.


