5.8: Kinetic Molecular Theory: Molecular Velocities, Temperature, and Kinetic Energy
The kinetic molecular theory qualitatively explains the behaviors described by the various gas laws. The postulates of this theory may be applied in a more quantitative fashion to derive these individual laws.
Collectively, the molecules in a sample of gas have average kinetic energy and average speed; but individually, they move at different speeds. Molecules frequently undergo elastic collisions in which the momentum is conserved. Since the colliding molecules are deflected off at different speeds, individual molecules have widely varying speeds. However, because of the vast number of molecules and collisions involved, the molecular speed distribution and average speed are constant. This molecular speed distribution is known as a Maxwell-Boltzmann distribution, and it depicts the relative numbers of molecules in a bulk sample of gas that possesses a given speed.
The kinetic energy (KE) of a particle of mass (m) and speed (u) is given by:
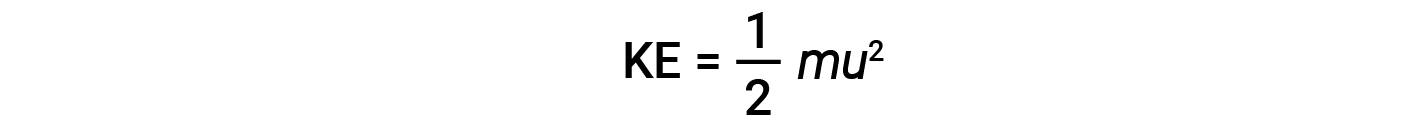
Expressing mass in kilograms and speed in meters per second will yield energy values in units of joules (J = kg·m2/s2). To deal with a large number of gas molecules, we use averages for both speed and kinetic energy. In the KMT, the root mean square velocity of a particle, urms, is defined as the square root of the average of the squares of the velocities with n = the number of particles:
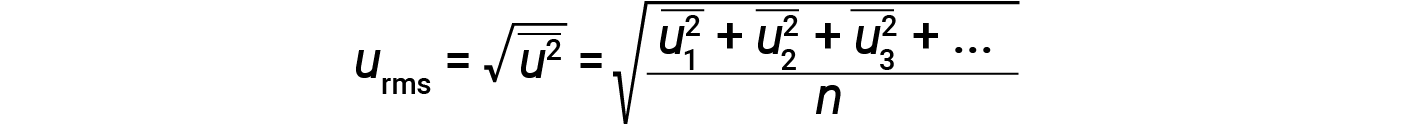
The average kinetic energy for a mole of particles, KEavg, is then equal to:
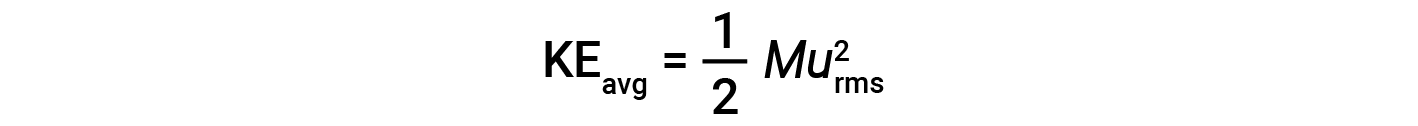
where M is the molar mass expressed in units of kg/mol. The KEavg of a mole of gas molecules is also directly proportional to the temperature of the gas and may be described by the equation:
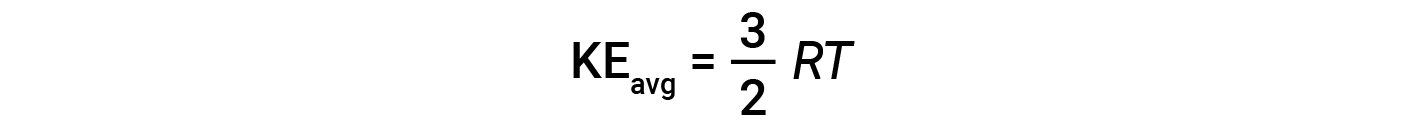
where R is the gas constant and T is the kelvin temperature. When used in this equation, the appropriate form of the gas constant is 8.314 J/mol⋅K (8.314 kg·m2/s2·mol·K). These two separate equations for KEavg may be combined and rearranged to yield a relationship between molecular speed and temperature:
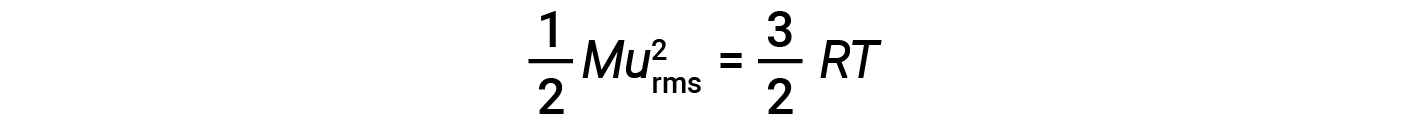
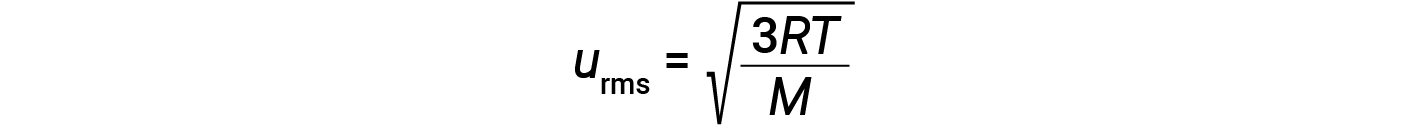
If the temperature of a gas increases, its KEavg increases, more molecules have higher speeds and fewer molecules have lower speeds, and the distribution shifts toward higher speeds overall, that is, to the right. If temperature decreases, KEavg decreases, more molecules have lower speeds and fewer molecules have higher speeds, and the distribution shifts toward lower speeds overall, that is, to the left.
At a given temperature, all gases have the same KEavg for their molecules. The molecular velocity of a gas is directly related to molecular mass. Gases composed of lighter molecules have more high-speed particles and a higher urms, with a speed distribution that peaks at relatively higher velocities. Gases consisting of heavier molecules have more low-speed particles, a lower urms, and a speed distribution that peaks at relatively lower velocities.
This text is adapted from Openstax, Chemistry 2e, Section 9.5: Kinetic-Molecular Theory.


