17.2: 熵
在水中加入溶解的 Salt 粒子从不会自发地回到溶液加入重新形成 Solid 粒子。 此外,一种在真空中膨胀的气体仍被分散,从未自动重组。 这些现象的单向性是热力学状态函数熵 (S) 的结果。 熵是衡量能量在整个系统中的分散程度的尺度,换句话说,它与热动力系统的无序度成正比。 熵可能会因系统的物理或化学变化而增加 (ΔS > 0 ,无序增加) 或减少 (ΔS < 0 ,无序减少)。 熵的变化是最终状态和初始状态的换向量之间的差值: ΔS = SF - Si。
博尔兹曼微状态理论
微状态是构成系统的原子或分子的所有位置和能量的特定配置。 系统的熵和可能的微酸盐 (W) 数量之间的关系是 S = k ln W ,其中 k 是博尔兹曼常数, 1.38 × 10−23 J/K
熵的变化是
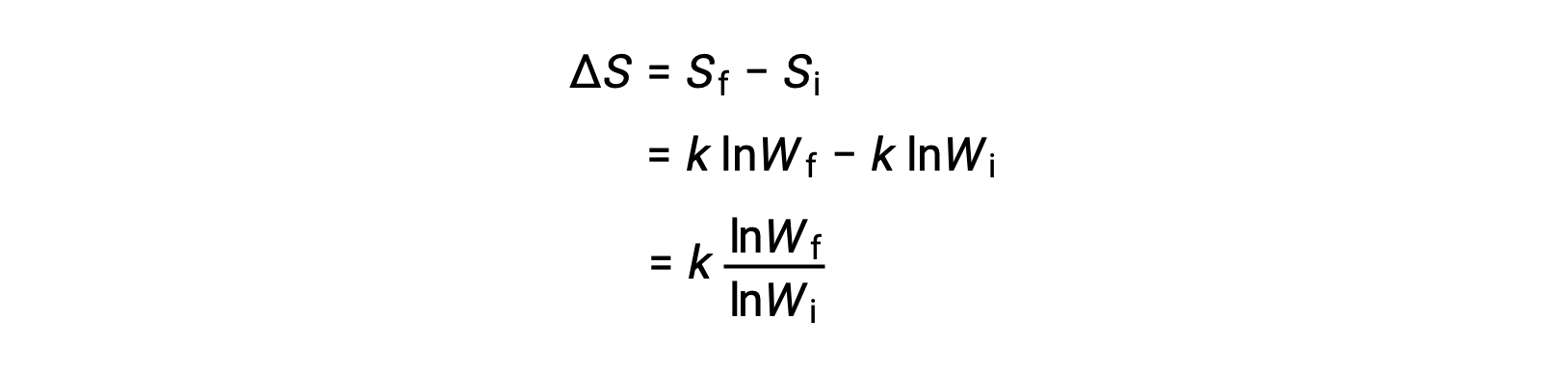
如果系统中可能存在的微量酸盐数量较多,则其无序性 (熵越高) 要高于有序系统 (熵越低) ,而微量酸盐的数量也就越少。 对于需要增加微状态数据 (WF > WI) 数量的过程,系统的熵会增加,而 ΔS > 0。 相反,减少微状态数据的进程, WF < WI ,产率 A Decrease in system 熵, ΔS < 0。
考虑两个连接的瓶之间理想气体的分布。 最初,气体分子仅限于两个瓶中的一个。 打开瓶间的阀门会增加气体分子可用的体积 (能量更分散在更大的域中) ,并相应增加系统可能的微酸盐数量。 由于 WF > WI ,扩展过程涉及熵的增加 (ΔS > 0) ,并且是自发的。
可以使用类似的方法来描述热的自发流动。 一杯热茶将其能量均匀地分散在冷却器室的更多空气粒子上,从而产生更多微酸盐。
关于熵的概括
熵,微量酸盐和物质 / 能量耗散之间的关系允许对物质的相对熵进行概括,并预测化学和物理过程中熵变化的迹象。
在固体相中,原子或分子被限制在彼此接近固定的位置,并且只能对这些位置进行微小的摆动。 因此,微量酸盐的数量相对较少。 在液相中,原子或分子可以自由地相互移动,尽管它们彼此之间的距离相对较近。 因此,固体的微酸盐数量相应为大于。 因此,液态 > 固态以及将物质从固体转化为液体 (熔化) 的过程的特征是熵增加, ΔS > 0。 根据相同的逻辑,对等过程 (凝固) 显示熵下降, ΔS 小于 0。
在气态相中, 给定数量的原子或分子所占的体积比液体相大得多,相当于微酸盐的数量大得多。 因此,对于任何物质,天然气 > 液体 > 固体,以及汽化和升华的过程也会增加熵, ΔS > 0。 同样,对等相位转换—冷凝和沉积—涉及熵的下降, ΔS < 0。
根据动能分子理论,一种物质的温度与其粒子的平均动能成正比。 提高物质温度将导致固体中粒子的外延的振动增加,并使粒子在液体和气体中的转换更快。 在较高的温度下,动能在物质原子或分子之间的分布也比在较低的温度下更为分散。 因此,任何物质的熵都会随着温度的升高而升高。
物质的熵受组成物质的粒子 (原子或分子) 结构的影响。 关于原子物质,在给定温度下,原子越重,熵越大,原子越轻,这是粒子质量与量化转化能量水平间距之间关系的结果。 对于分子,原子数量的增加会增加分子振动的方式,从而增加可能的微酸盐数量和系统的熵。
最后,粒子类型的变化会影响系统的熵。 与所有粒子均相同的纯物质相比,两种或两种以上不同粒子类型混合物的熵更大。 这是因为在由非相同组件组成的系统中可能有更多的方向和交互。 例如,当固体溶解在液体中时,固体的粒子会有更大的运动自由度,并与溶剂粒子发生额外的交互。 这对应于更均匀的物质和能量的耗散和更多的微酸盐。 因此,溶解的过程涉及到熵的增加, ΔS > 0。
本文改编自 Openstax, 化学 2e, 第 16.2 章:熵。


