14.3: 气态反应和非均相反应的平衡
用于气态反应的均质平衡
对于气相反应,平衡常数可以用反应物和生成物的摩尔浓度 (KC) 或分压 (KP) 表示。 这两个K 值之间的关系可以简单地从理想的气体方程和体积摩尔浓度的定义中导出。 根据理想的气体方程:
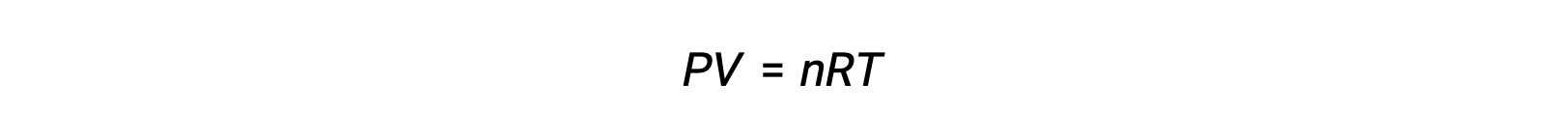
摩尔浓度或体积摩尔浓度由摩尔数除以体积:
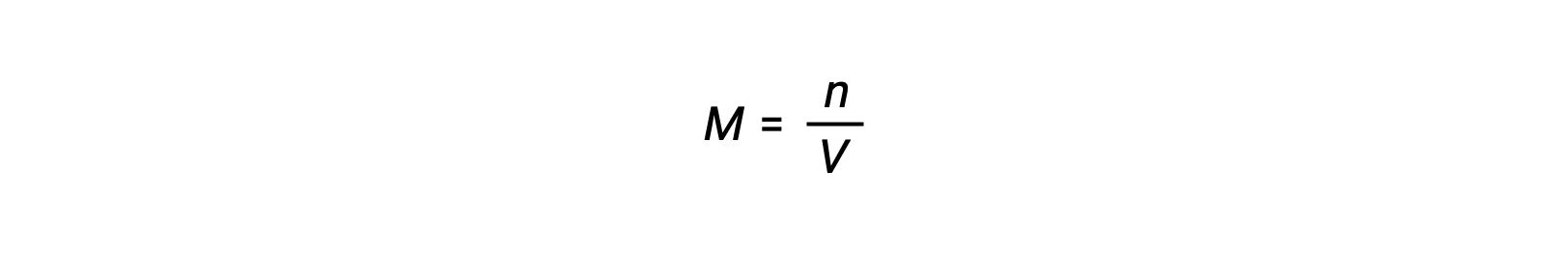
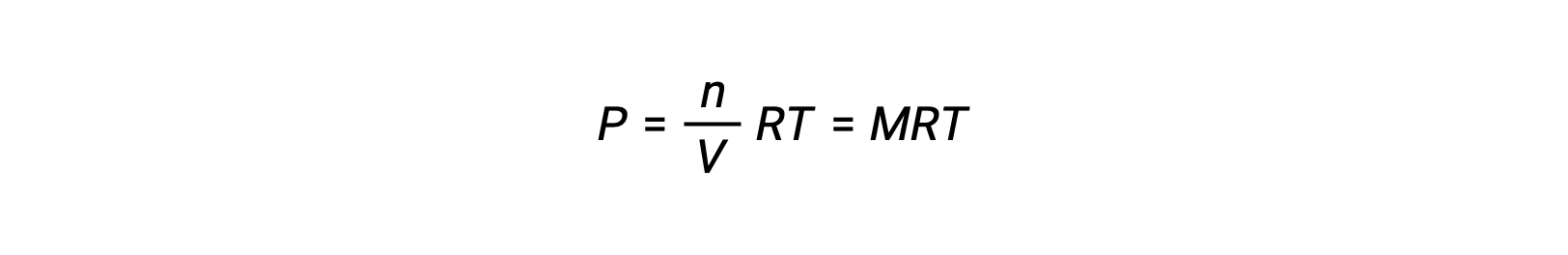
其中 P 是部分压力, V 是体积, n 是摩尔数, R 是气体常数, T 是温度, M 是摩尔浓度。
对于气相反应: M A + n B ⇌ x C + y D
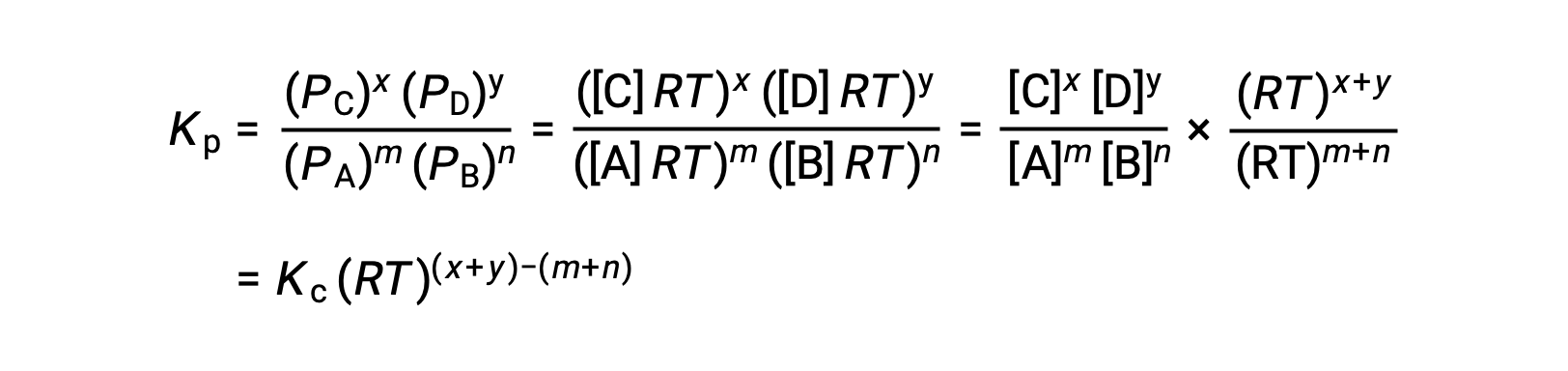
因此,KC 和 KP 之间的关系是
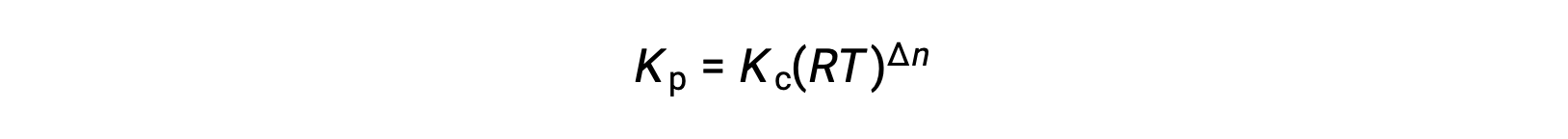
其中 Δn 是生成物和反应物气体的摩尔量的差异,在本例中:
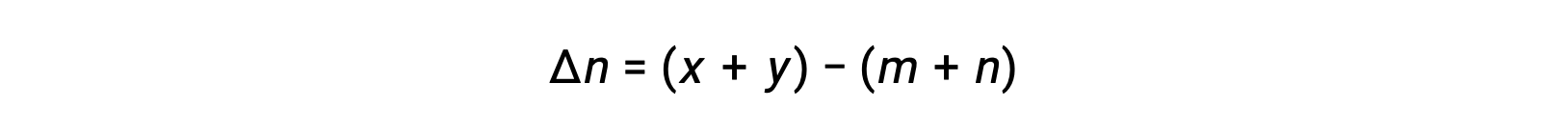
本文改编自 Openstax, 化学 2e, 第 13.2 节:平衡常数。


