12.8: Vapor Pressure Lowering
The equilibrium vapor pressure of a liquid is the pressure exerted by its gaseous phase when vaporization and condensation are occurring at equal rates:
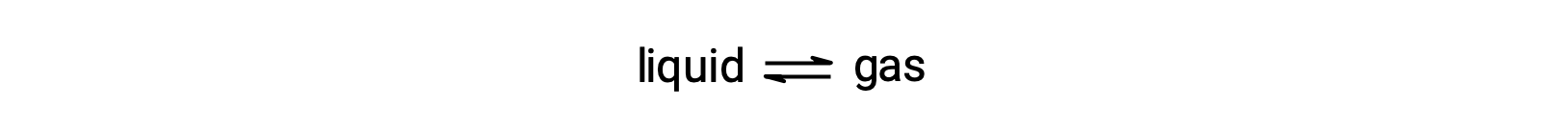
Dissolving a nonvolatile substance in volatile liquid results in a lowering of the liquid’s vapor pressure. This phenomenon can be explained by considering the effect of added solute molecules on the liquid's vaporization and condensation processes. To vaporize, solvent molecules must be present at the surface of the solution. The presence of solute decreases the surface area available to solvent molecules and thereby reduces the rate of solvent vaporization. Since the rate of condensation is unaffected by the presence of solute, the net result is that the vaporization-condensation equilibrium is achieved with fewer solvent molecules in the vapor phase (i.e., at a lower vapor pressure).
While this interpretation is useful, it does not account for several important aspects of the colligative nature of vapor pressure lowering. A more rigorous explanation involves the property of entropy. For purposes of understanding the lowering of a liquid's vapor pressure, it is adequate to note that the more dispersed nature of matter in a solution, compared to separate solvent and solute phases, serves to effectively stabilize the solvent molecules and hinder their vaporization. A lower vapor pressure results, and a correspondingly higher boiling point.
The relationship between the vapor pressures of solution components and the concentrations of those components is described by Raoult’s law: The partial pressure exerted by any component of an ideal solution is equal to the vapor pressure of the pure component multiplied by its mole fraction in the solution.
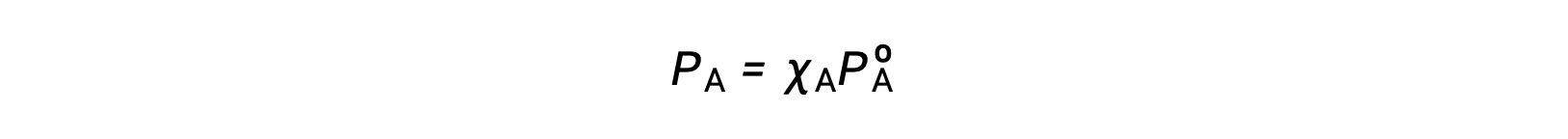
where PA is the partial pressure exerted by component A in the solution, PºA is the vapor pressure of pure A, and XA is the mole fraction of A in the solution.
Recalling that the total pressure of a gaseous mixture is equal to the sum of partial pressures for all its components (Dalton’s law of partial pressures), the total vapor pressure exerted by a solution containing i components is
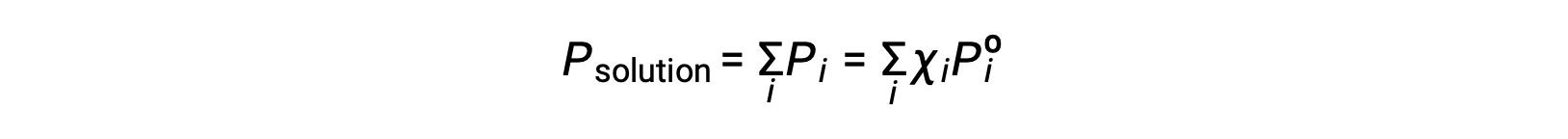
A nonvolatile substance is one whose vapor pressure is negligible (Pº ≈ 0), and so the vapor pressure above a solution containing only nonvolatile solutes is due only to the solvent:
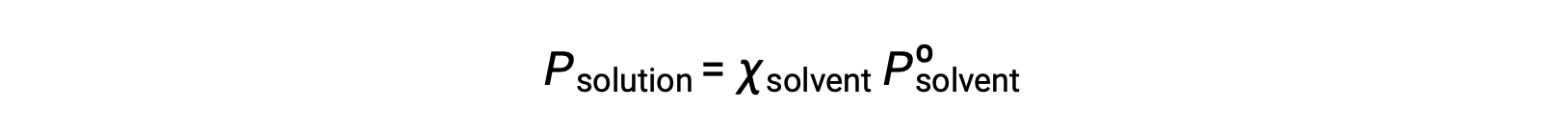
This text is adapted from Openstax, Chemistry 2e, Section 11.4: Colligative Properties.


