17.6: Enthalpie libre
L'un des défis lorsqu'on utilise le deuxième principe de la thermodynamique pour déterminer si un processus est spontané est qu'il nécessite des mesures de la variation d'entropie du système et de la variation d'entropie de l'environnement extérieur. Une autre approche possible impliquant une nouvelle propriété thermodynamique définie seulement en termes de propriétés du système a été introduite à la fin du XIXe siècle par le mathématicien américain Josiah Willard Gibbs. Cette nouvelle propriété est appelée l'énergie libre de Gibbs (G) (ou simplement énergie libre), et elle est définie en termes d'enthalpie et d'entropie d'un système comme suit :
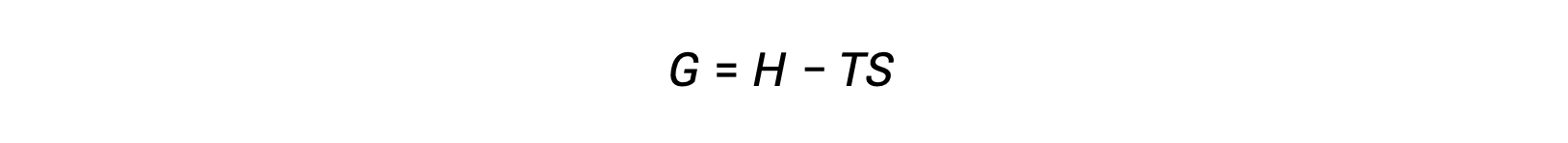
L'énergie libre est une fonction d'état, et à une température et une pression constantes, la variation d'énergie libre (ΔG) peut être exprimée comme suit :
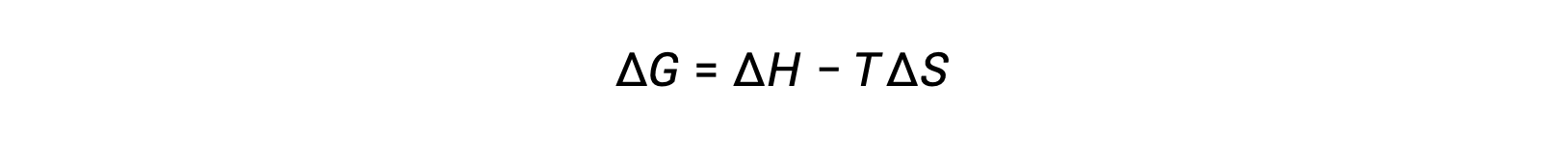
On peut comprendre la relation entre cette propriété du système et la spontanéité d'un processus en se rappelant l'expression du deuxième principe déduite précédemment :
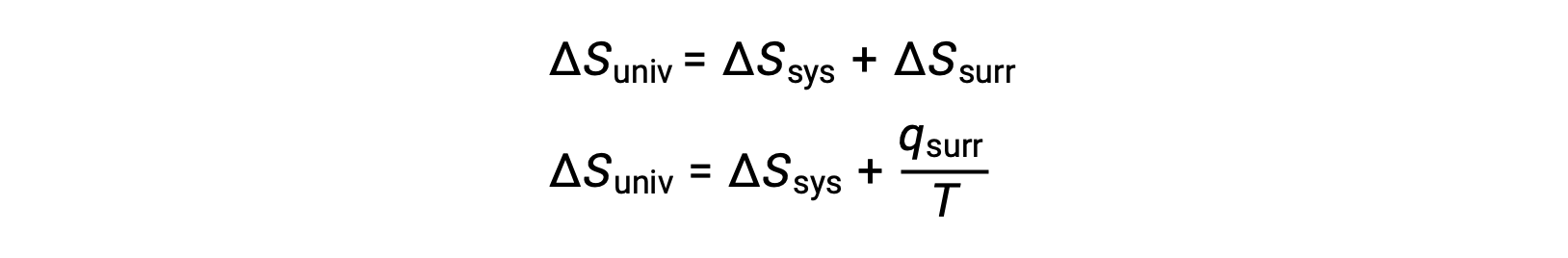
Le premier principe exige que qext = −qsys, et à pression constante qsys = ΔH, de sorte que cette expression peut être réécrite comme suit :
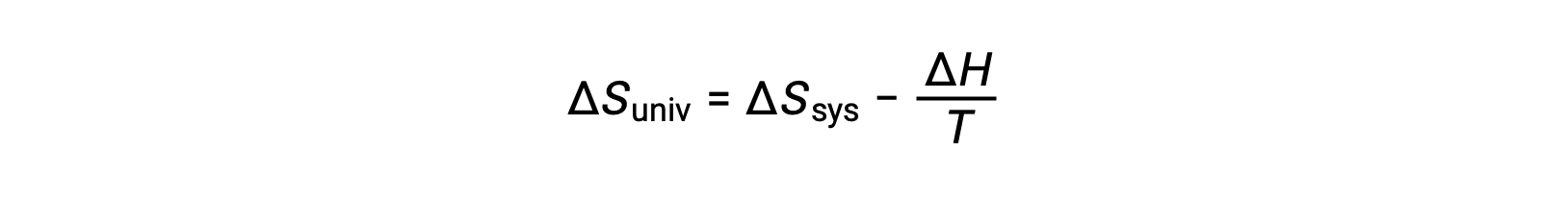
En multipliant les deux côtés de cette équation par −T et en réorganisant, on obtient ce qui suit :
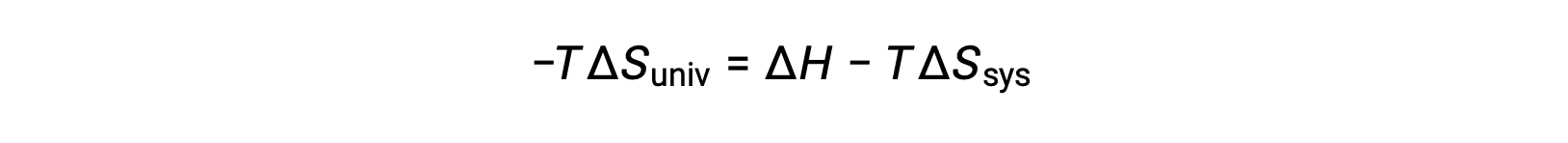
Pour des raisons de simplicité, l’indice “ sys ” peut être omis et l’expression devient
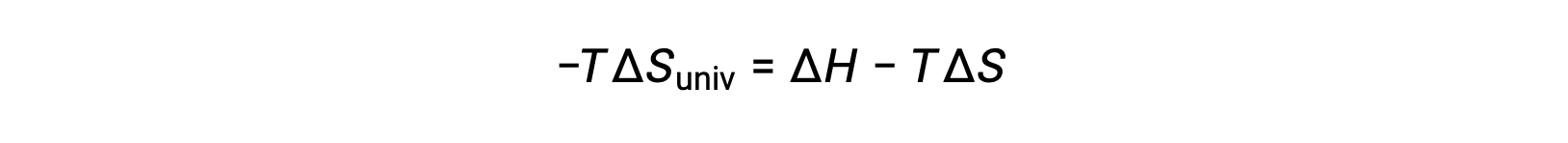
La comparaison de cette équation à la précédente pour la variation d'énergie libre montre la relation suivante :
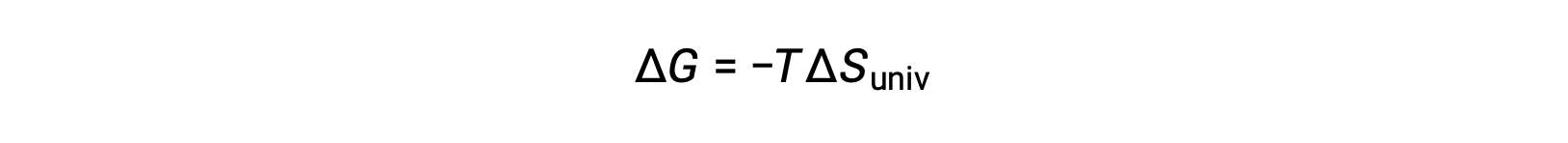
La variation d'énergie libre est donc un indicateur fiable de la spontanéité d'un processus, car il est directement lié à l'indicateur de spontanéité identifié précédemment, ΔSuniv.
Si ΔSuniv > 0, ΔG < 0 et la réaction est spontanée.
Si ΔSuniv < 0, ΔG > 0 et la réaction est non spontanée.
Si ΔSuniv = 0, ΔG = 0 et la réaction est à l'équilibre.
Ce texte est adapté de Openstax, Chimie 2e, Chapitre 16.4 : Énergie libre.


