13.8: Tracés d'Arrhenius
La loi d'Arrhénius relie l'énergie d'activation et la constante de vitesse, k, pour les réactions chimiques. Dans l'équation d'Arrhénius, k = Ae−Ea/RT, R est la constante du gaz parfait, qui a une valeur de 8,314 J/mol·K, T est la température sur l'échelle de Kelvin, Ea est l'énergie d'activation en J/mole, e est la constante 2,7183 et A est une constante appelée le facteur de fréquence, qui est lié à la fréquence des chocs et à l'orientation des molécules qui réagissent.
L'équation d'Arrhénius peut être utilisée pour calculer l'énergie d'activation d'une réaction à partir de données cinétiques expérimentales. Une approche pratique pour déterminer l'Ea d'une réaction implique la mesure de k à deux ou plusieurs températures différentes. Elle utilise une version modifiée de l'équation d'Arrhénius qui prend la forme d'une équation linéaire :
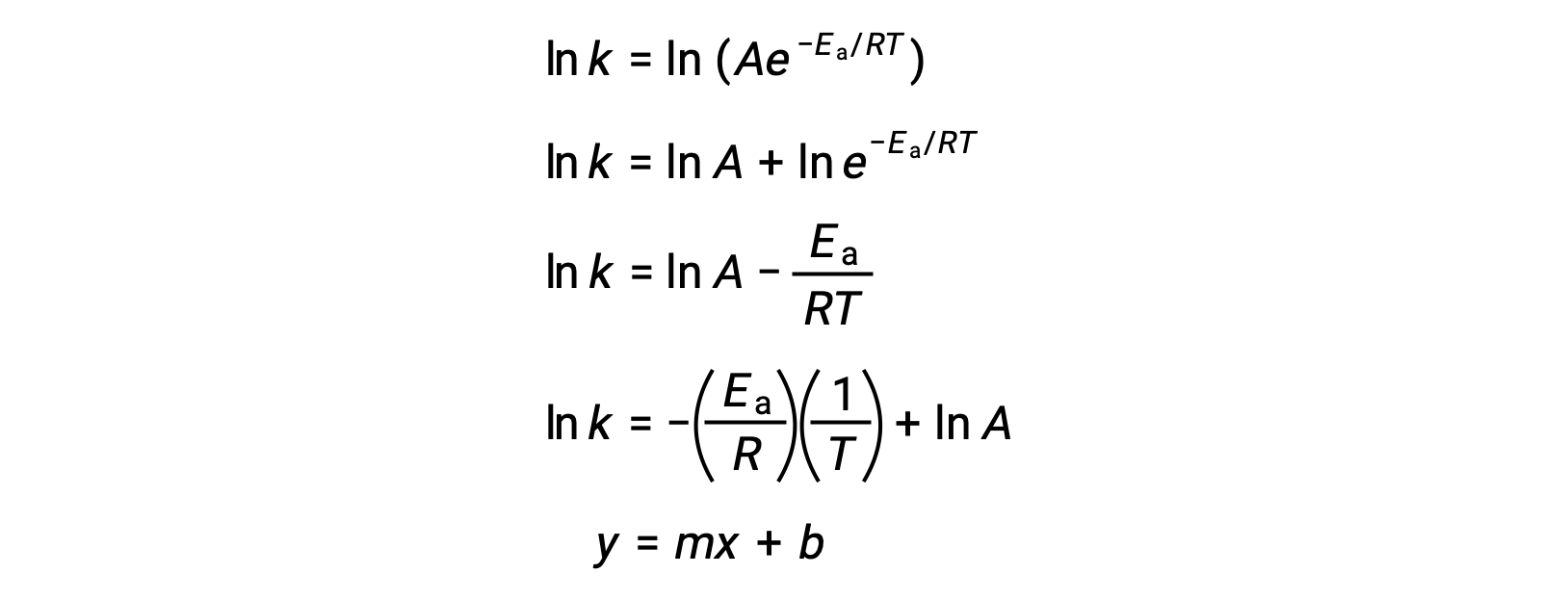
Un tracé de ln k par rapport à 1/T est linéaire, avec une pente égale à −Ea/R et une ordonnée à l'origine égale à ln A.
Réfléchissez à la réaction suivante :
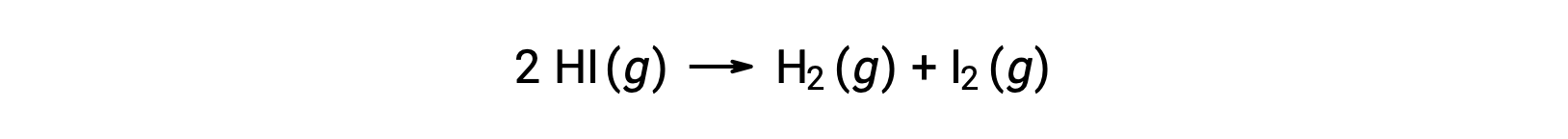
L'énergie d'activation de cette réaction peut être déterminée si la variation de la constante de vitesse avec la température est connue à partir des données cinétiques de la réaction, comme illustré.
| Température (K) | Constante de vitesse (L/mol/s) |
| 555 | 3,52 × 10–7 |
| 575 | 1,22 × 10–6 |
| 645 | 8,59 × 10–5 |
| 700 | 1,16 × 10–3 |
| 781 | 3,95 × 10–2 |
Les données fournies peuvent être utilisées pour déduire les valeurs de l'inverse de la température (1/T) et du logarithme népérien de k (ln k).
| 1/T (K–1) | ln k |
| 1,80 × 10–3 | –14,860 |
| 1,74 × 10–3 | –13,617 |
| 1,55 × 10–3 | –9,362 |
| 1,43 × 10–3 | –6,759 |
| 1,28 × 10–3 | –3,231 |
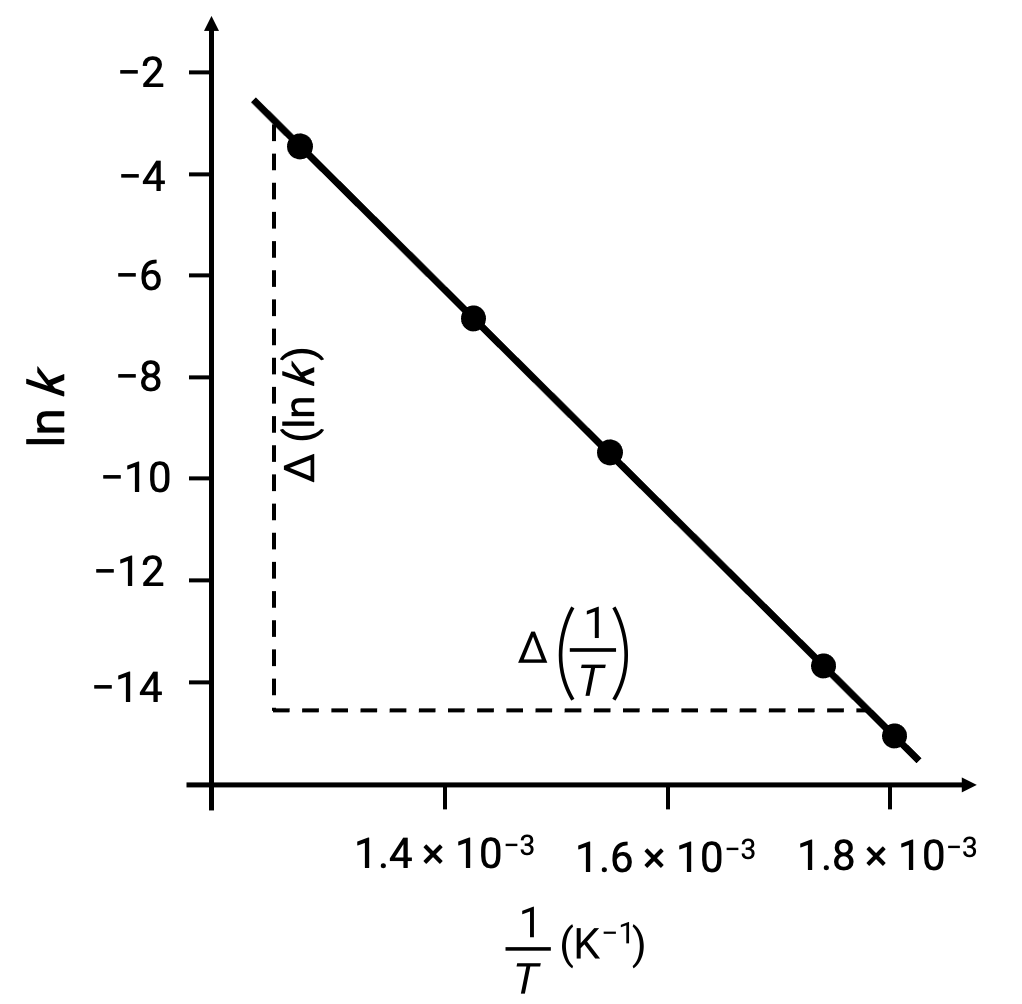
En traçant les points déduits des données avec ln k par rapport à 1/T, un graphe linéaire présentant une relation linéaire entre ln k et 1/T est généré, comme illustré.
La pente de la droite, qui correspond à l'énergie d'activation, peut être estimée à l'aide de deux des paires de données expérimentales.

Une autre approche pour déduire l'énergie d'activation implique l'utilisation de la constante de vitesse à deux températures différentes. Pour cette approche, l'équation d'Arrhenius est réorganisée sous une forme à deux points pratique :
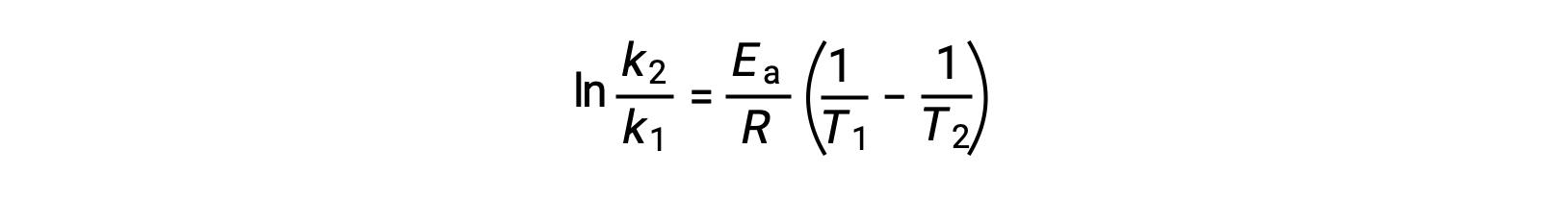
Lors de la réorganisation de l'équation, une expression pour l'énergie d'activation est générée.
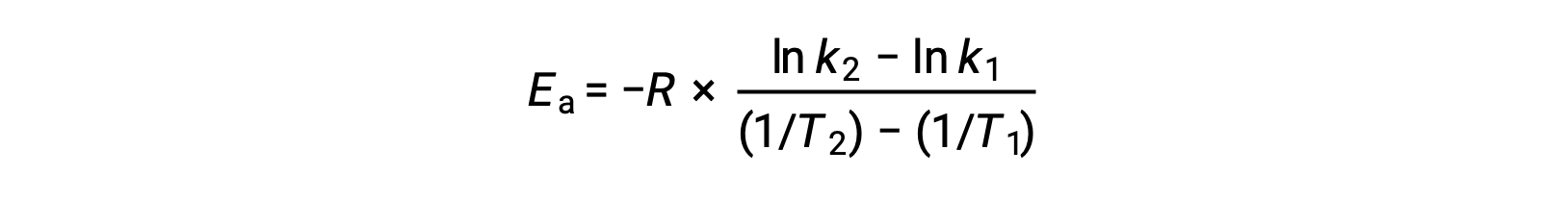
En substituant deux paires de données et en effectuant davantage de calculs, on obtient la valeur de l'énergie d'activation en joules par mole ou kilojoules par mole.
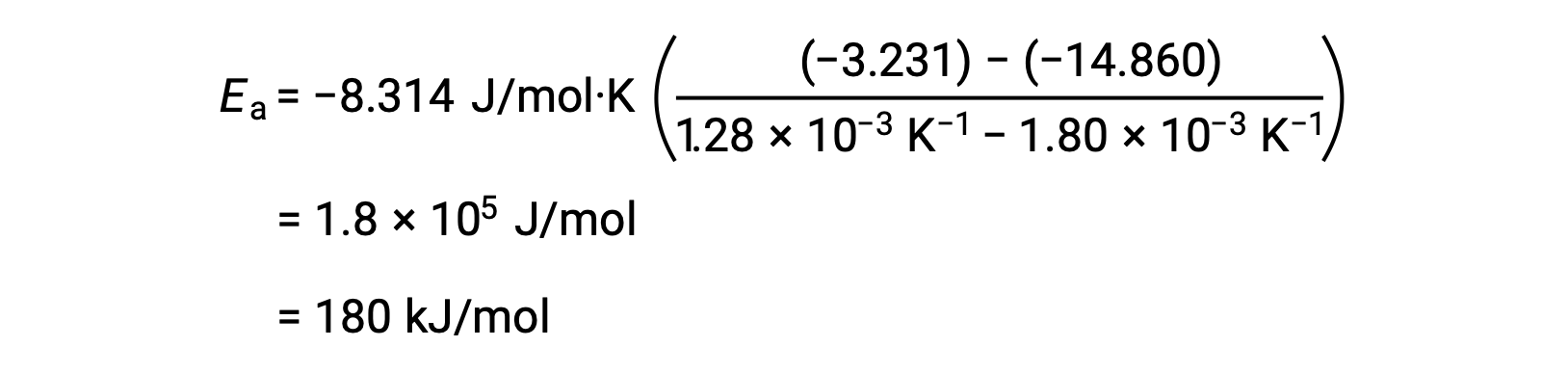
Cette autre approche à deux points donne le même résultat que l'approche graphique. Cependant, dans la pratique, l'approche graphique fournit généralement des résultats plus fiables tout en travaillant avec des données expérimentales réelles.
Ce texte est adapté de Openstax, Chimie 2e, Section 12.5 : Théorie des collisions.


